สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
พบกันอีกครั้งหนึ่งในบ่ายวันจันทร์แบบนี้ วันนี้ผมจะขออนุญาตมาทำการโพสต์และแชร์ความรู้เกี่ยวกับเรื่อง การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา มาฝากเพื่อนๆ ทุกคนนะครับ
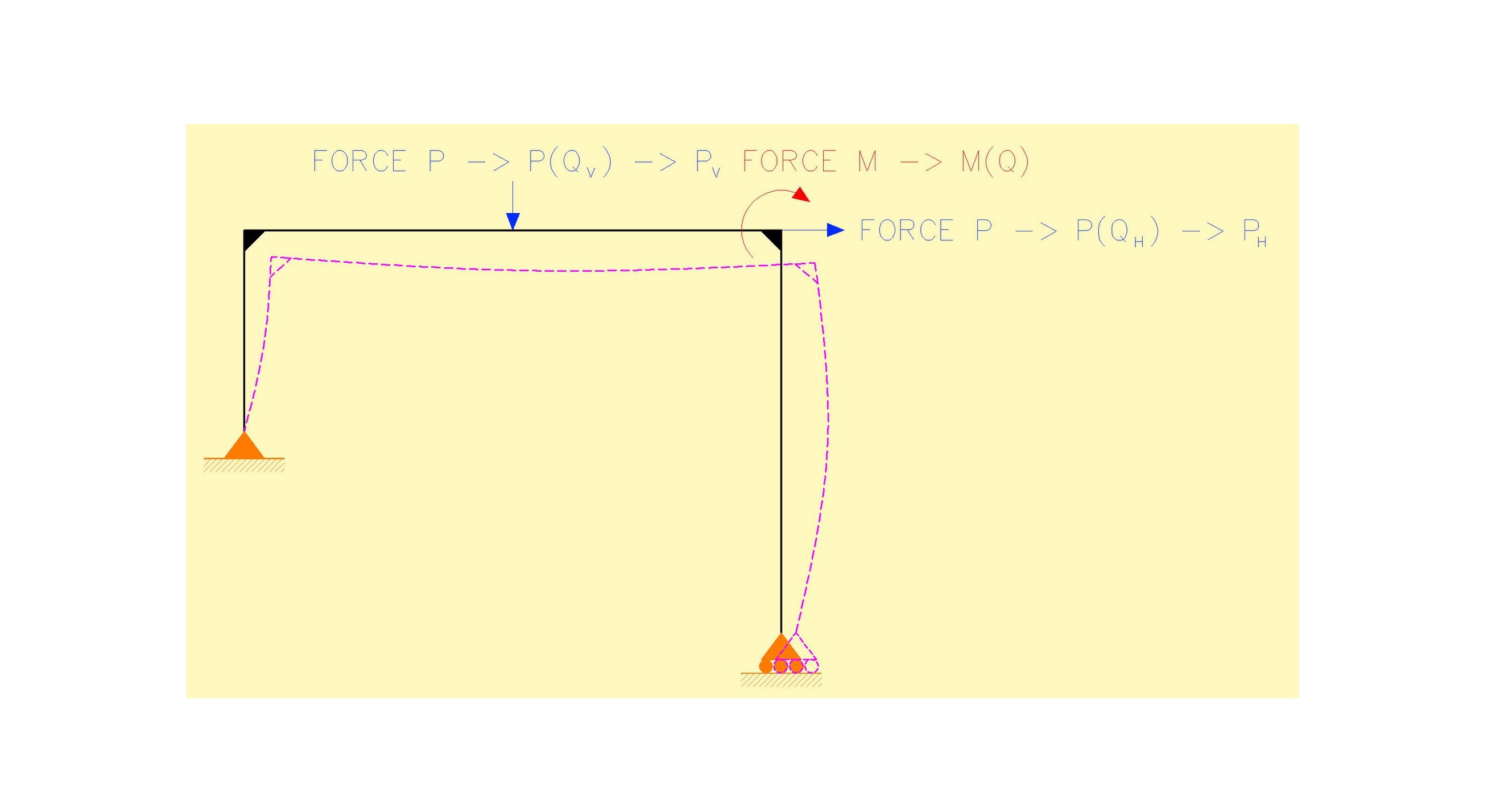
วันนี้ผมจะขออนุญาตมาทำการอธิบายวิธีในการประยุกต์ใช้วิธีการ CASTIGLIANO’S 2ND THEOREM สำหรับกรณีที่เรามีความต้องการที่จะทำการวิเคราะห์หาค่าการเสียรูป ซึ่งจะรวมไปถึงค่าระยะของการโก่งตัวและค่ามุมหมุนที่เกิดขึ้นภายในโครงสร้างโครงข้อแข็งแบบ 2 มิติ หรือว่า PLANE RIGID FRAME แก่เพื่อนๆ โดยที่เพื่อนๆ สามารถที่จะดูรูปตัวอย่างประกอบคำอธิบายของผมได้นะครับ
จากรูปๆ นี้เมื่อเราต้องการที่จะทำการหาค่าการเสียรูปที่ตำแหน่งใดตำแหน่งหนึ่งบนโครงสร้างโครงข้อแข็งๆ นี้เราก็จะทำการ สมมติ ว่ามีแรงกระทำ Q ในทิศทางของการเสียรูปที่เราสนใจนะครับ ตัวอย่างเช่น หากต้องการระยะโก่งในแนวดิ่งที่ตำแหน่งหนึ่งๆ เราก็สมมติให้แรงในแนวดิ่ง Q กระทำในทิศทางที่เราคาดว่าจะมีการโก่งตัว ณ ตำแหน่งที่เราสนใจนั้นๆ หากต้องการหามุมหมุนที่ตำแหน่งหนึ่งๆ เราก็สมมติให้แรงโมเมนต์ Q กระทำในทิศทางที่เราคาดว่าจะมีการหมุนไปในทิศทางนั้น ณ ตำแหน่งที่เราสนใจนั้นๆ เป็นต้น
ปล 1: ไม่ต้องกังวลไปนะครับว่าการแทนด้วยทิศทางใดๆ หากเราสมมติทิศทางผิดไป คำตอบก็จะออกมาเป็นค่าติดลบ แสดงให้เห็นว่าการแทนทิศทางผิดไป แค่นั้นเองครับ
ปล 2: หากตำแหน่งนั้นๆที่เราด้วยแรง Q ไป มีแรงกระทำอยู่แล้ว ก็ให้ทำตามขั้นตอนไปก่อนนะครับ พอในท้ายที่สุดแล้วก็ให้แทนแรง Q นี้ด้วยแรงที่มีอยู่แล้วได้เลยครับ และหากที่แรง Q นี้ไม่มีแรงกระทำใดๆเลย ก็ให้ทำเช่นเดียวกันครับ เพียงแต่ในท้ายที่สุดแล้วก็ให้แรง Q นั้นๆเท่ากับ 0 แค่นั้นเองครับ
ต่อมาก็ให้ทำการวิเคราะห์หาแรง REACTIONS ต่างๆของโครงสร้าง โดยให้ถือว่าแรง Q ที่สมมตินั้นเสมือนแรงๆ หนึ่งในระบบโครงสร้าง ดังนั้นค่า REACTIONS ต่างๆจะมีค่าของแรง Q นี้รวมอยู่ด้วยและสิ่งๆ หนึ่งที่ถือได้ว่าเป็นเอกลักษณ์ที่เพื่อนๆ จะต้องพบเจอหากทำการแก้ปัญหาค่าการเสียรูปภายในโครงสร้างโครงข้อแข็งนั่นก็คือ เราจะต้องทำการคำนวณหา INTERNAL FORCE ต่างๆ ที่จะเกิดขึ้นภายในทุกๆ RIGID JOINT ของโครงสร้างโครงข้อแข็ง จากนั้นก็ให้เราทำการเขียนพจน์ของพลังงานค่าของความเครียด U ว่าโครงสร้างที่กำหนดให้นั้นจะมีผลจากการกระทำของแรงอะไรบ้างและก็ทำการหาค่าการเสียรูปต่างๆ โดยที่เทอมต่างๆ ก็จะเหมือนๆ กัน คือ การรวมผลต่างๆ (∑, ∫) ของผลคูณระหว่างค่าแรงในรูปแบบต่างๆ เช่น N (แรงตามแนวแกน) M (แรงดัด) V (แรงเฉือน) T (แรงบิด) เป็นต้น คูณกับค่า PARTIAL DERIVATIVE ของแรงนั้นๆ เทียบกับค่าแรงที่เราทำการสมมติขึ้น หารด้วยค่าความแข็งแกร่งของโครงสร้างที่มีต่อแรงนั้นๆ (RIGIDITY) ซึ่งก็จะสอดคล้องกับแรงที่เราทำการพิจารณาในพจน์นั้นๆ เช่น ในเทอมของแรงตามแนวแกน ค่า AXIAL RIGIDITY มีค่าเท่ากับ AE/L เทอมของแรงดัด ค่า FLEXURAL RIGIDITY มีค่าเท่ากับ EI เทอมของแรงเฉือน ค่า SHEAR RIGIDITY มีค่าเท่ากับ AG เทอมของแรงบิด ค่า TORSIONAL RIGIDITY มีค่าเท่ากับ GK เป็นต้น
ดังนั้นสำหรับค่าเสียรูปซึ่งในที่นี้คือ ค่าการโก่งตัวในทิศทางใดทิศทางหนึ่งของโครงสร้างโครงข้อแข็งนั้นจะสามารถทำการคำนวณและหาได้จาก
Δ = ∂U/∂P(Q)
Δ = ∑(N)[∂N/∂P(Q)](L/AE)+∑∫(M)[∂M/∂P(Q)]/(EI)dx+∑∫(λV)[∂V/∂P(Q)]/(AG)dx+∑∫(T)[∂T/∂P(Q)]/(GK)dx+…
และสำหรับค่าเสียรูปซึ่งในที่นี้คือ ค่ามุมหมุนในทิศทางใดทิศทางหนึ่งของโครงสร้างโครงข้อแข็งนั้นเราก็จะสามารถทำการคำนวณและหาได้เช่นกันจาก
θ = ∂U/∂M(Q)
θ = ∑(N)[∂N/∂M(Q)](L/AE)+∑∫(M)[∂M/∂M(Q)]/(EI)dx+∑∫(λV)[∂V/∂M(Q)]/(AG)dx+∑∫(T)[∂T/∂M(Q)]/(GK)dx+…
พอเราทำการรวมค่าหรือการอินทิเกรตทั้งหมดเสร็จแล้ว ก็ให้แทนค่าว่า P(Q) หรือ M(Q) ที่เราสมมตินั้นมีหรือไม่มีแรงกระทำอยู่ หากมีก็ให้แทนลงไป หากไม่มีก็ให้มีค่าเท่ากับ 0 ได้เลยและอย่างที่เรียนไปว่า ด้วยวิธีการนี้เราไม่ต้องกังวลเรื่องทิศทางที่เราทำการสมมติขึ้น เพราะหากเราทำการสมมติผิดคำตอบก็จะเป็นตัวฟ้องในขั้นตอนสุดท้ายนี้เองเลยครับ
เป็นยังไงบ้างครับ ง่ายมากๆ เลยใช่มั้ยละครับ? หากอ่านที่ผมอธิบายแล้วไม่เข้าใจตรงไหนก็ไม่เป็นไร ผมจะขอรบกวนให้เพื่อนๆ นั้นทำการสอบถามกันเข้ามาใต้โพสต์ๆ นี้หรือจะในอินบ็อกซ์ของทางเพจก็ได้นะครับ เอาเป็นว่าในครั้งหน้าที่เราพบกัน ผมจะทำตัวอย่างในการวิเคราะห์หาค่าการเสียรูปของโครงสร้างโครงสร้างโครงข้อแข็งให้เพื่อนๆ ได้รับชมและทำความเข้าใจร่วมกัน ยังไงหากเพื่อนๆ ท่านใดที่มีความสนใจในหัวข้อๆ นี้เป็นพิเศษก็อย่าลืมติดตามกันได้นะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา
#อธิบายหลักการวิเคราะห์หาค่าการโก่งตัวของโครงสร้างโครงข้อแข็งโดยวิธีทฤษฏีที่2ของคาสติเกลียโน่
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com