สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
พบกันอีกครั้งหนึ่งในบ่ายวันจันทร์แบบนี้ วันนี้ผมจะขออนุญาตมาทำการโพสต์และแชร์ความรู้เกี่ยวกับเรื่อง การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา มาฝากเพื่อนๆ ทุกคนนะครับ
(รูปที่1)
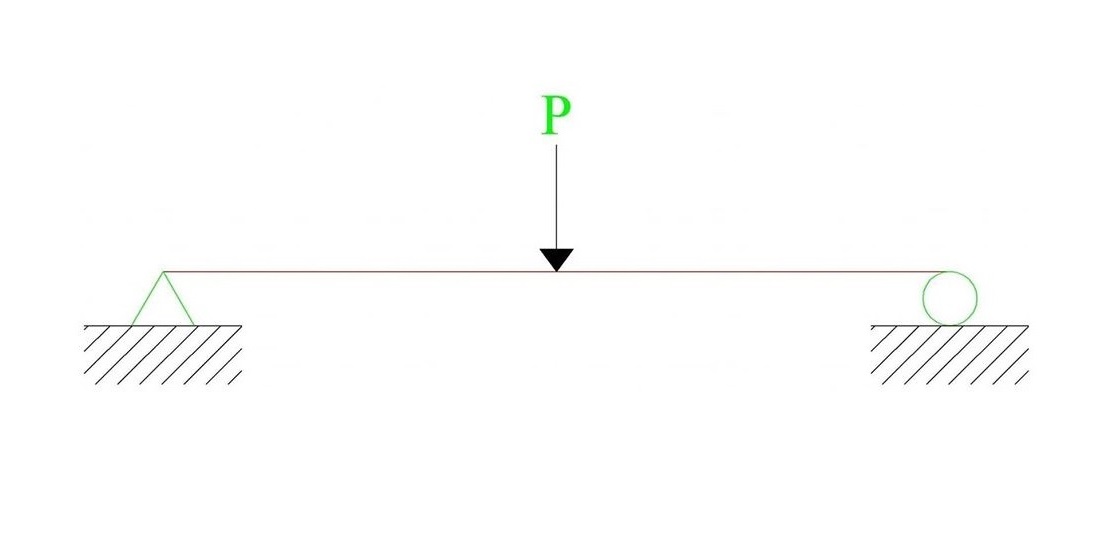
ผมจะขออนุญาตเริ่มต้นโดยทำการ DERIVE สมการตั้งต้นของ CASTIGLIANO’S 2ND THEOREM ให้ทุกๆ ท่านได้ทราบกันก่อน เพื่อนๆ จะได้เข้าใจที่มาที่ไปของสมการตั้งต้นตัวนี้ เพื่อการประยุกต์ใช้งานที่ถูกต้องต่อไป โดยที่ผมอยากจะขอยก ตย คานช่วงเดียว (SIMPLE BEAM) ที่มีการรับน้ำหนักบรรทุกแบบจุด (CONCENTRATED LOAD) ตามรูปที่ 1 นะครับ
(รูปที่2)
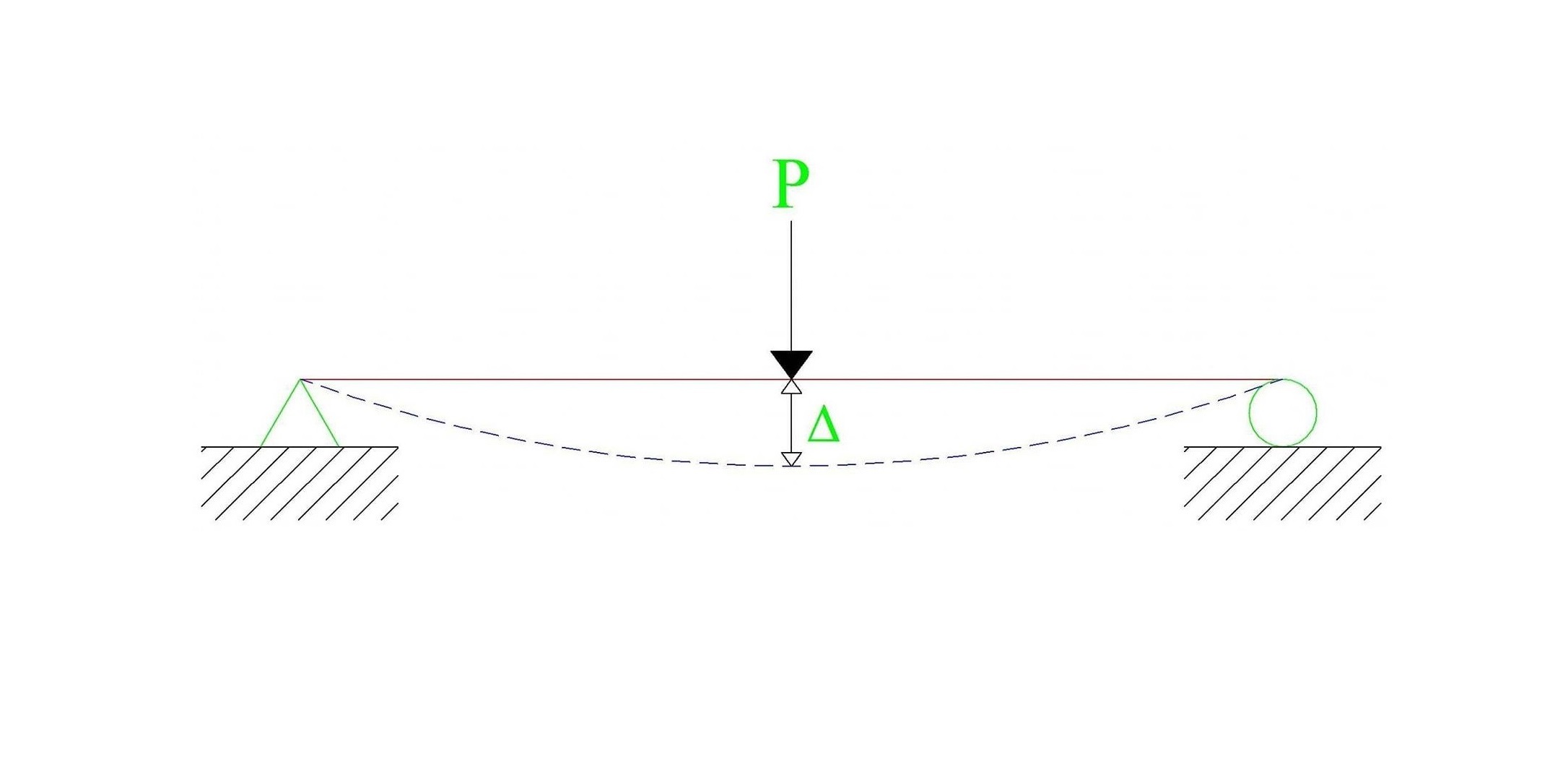
ในรูปที่ 2 เราจะสามารถเห็นได้ว่าเมื่อคานของเราเริ่มที่จะรับน้ำหนัก ก็จะทำให้เกิดการเสียรูปอันเนื่องมาจากแรง P ซึ่งมีค่าเท่ากับ Δ นะครับ
(รูปที่3)
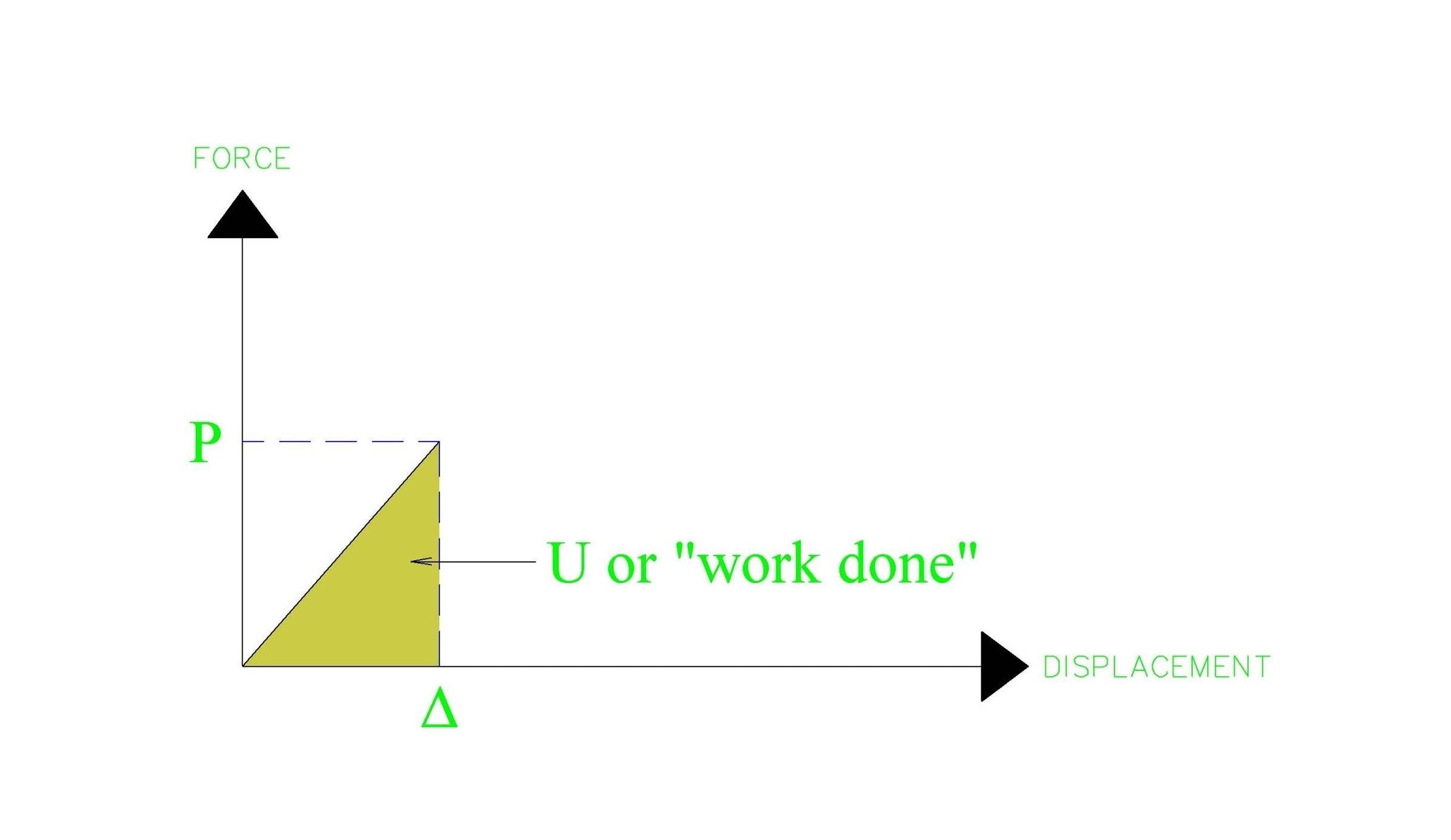
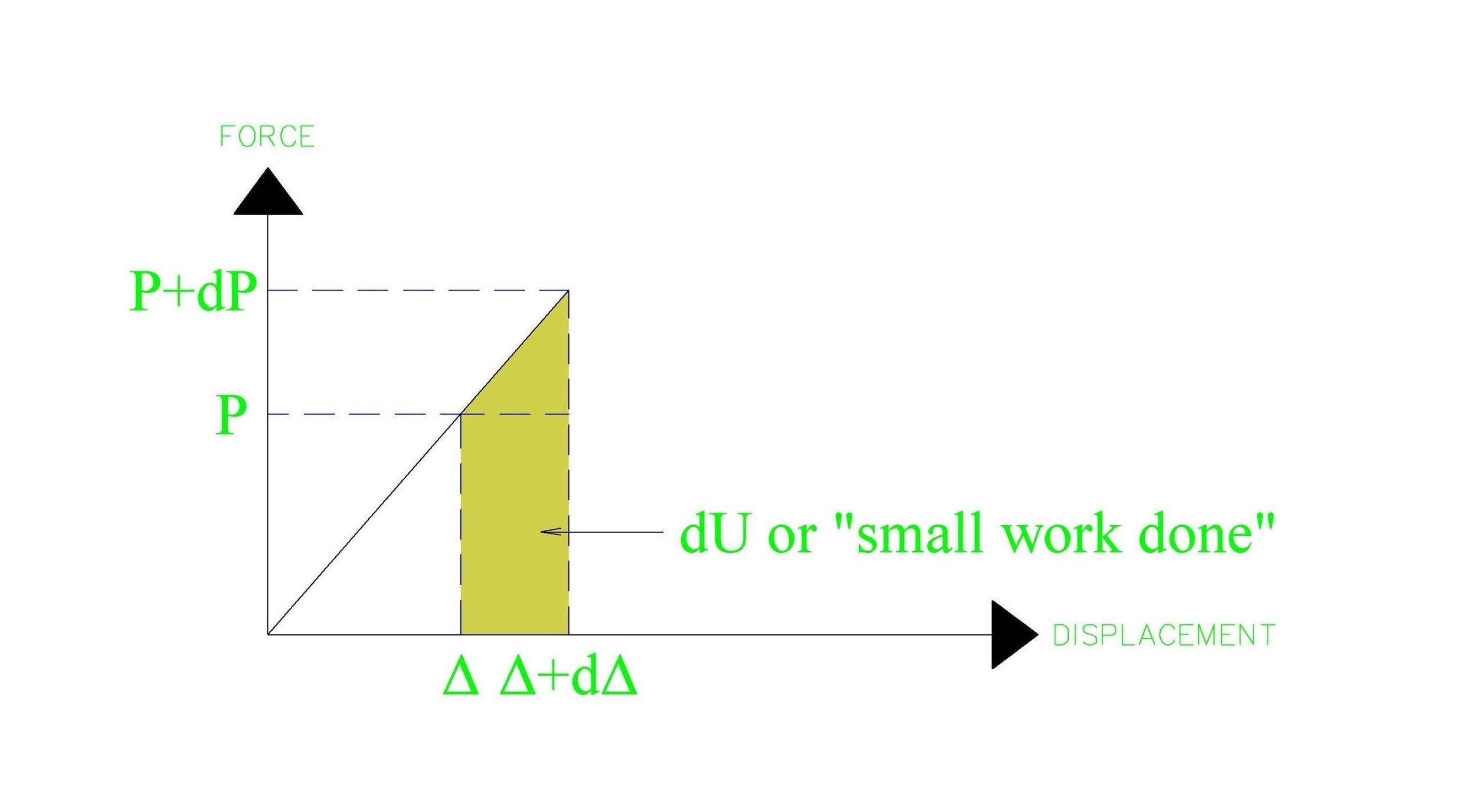
จากกฎอนุรักษ์พลังงาน พลังงานความเครียดที่สะสมภายในคาน หรือค่า U (STRAIN ENERGY) เราสามารถที่จะเขียนให้ค่าดังกล่าวอยู่ในรูปสมการโดยคำนวณจากพื้นที่ใต้กราฟของแผนภูมิแสดงความสัมพันธ์ระหว่างค่าการเสียรูปกับแรงกระทำได้แสดงเอาไว้ในรูปที่ 3 นะครับ ซึ่งเราจะสามารถเขียนให้อยู่ในรูปของสมการได้ว่า
U = ½ (P)(Δ) …สมการที่ 1
(รูปที่4)
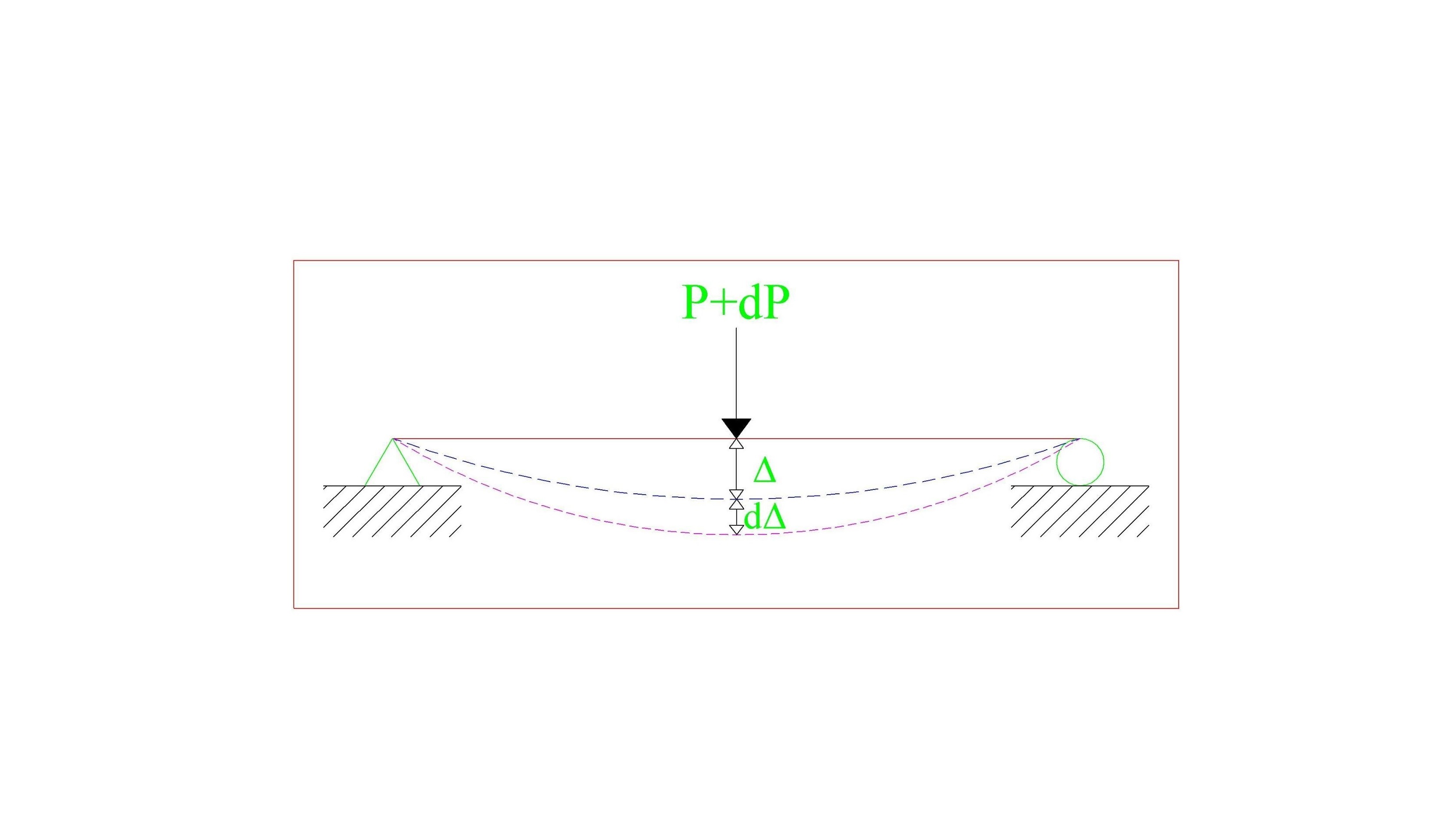
ต่อมาหากว่าเราต้องการที่จะหาระยะการโก่งตัวในแนวดิ่ง (VERTICAL DISPLACEMENT) ที่ตำแหน่งนี้ เราก็จะค่อยๆ ทำการเพิ่มค่าน้ำหนักบรรทุกตัวนี้อีกเล็กน้อยโดยสมมติว่าค่าน้ำหนักที่เพิ่มขึ้นนี้มีค่าเท่ากับ dP ซึ่งสิ่งที่จะเกิดตามมาก็คือ ค่าการเสียรูปอีกเล็กน้อยเช่นกันซึ่งมีค่าเท่ากับ dΔ ตามรูปที่ 4 นะครับ
(รูปที่5)
จากรูปที่ 5 ข้างล่างเราจะสามารถหาค่าพลังงานสะสมภายในคานที่เพิ่มขึ้นอีกเท่ากับ dU อันเนื่องมาจากการกระทำของแรง dP สามารถเขียนในรูปของสมการได้ว่า
dU = ½ (dΔ)(dP)+(P)(dΔ)
dU = 0+(P)(dΔ)
dU = (P)(dΔ) …สมการที่ 2
จากนั้นหากเรารวมพลังงานความเครียดทั้งหมดจะได้ว่า
Ut = U + dU
Ut = ½ (P)(Δ)+(P)(dP) …สมการที่ 3
ต่อมาหากเราทำการพิจารณาความสัมพันธ์โดยรวมระหว่างแรงกระทำกับการเสียรูปที่เกิดขึ้น เราสามารถหาค่าพลังงานความเครียดทั้งหมดที่ได้จากงานภายนอกและสามารถเชียนออกมาได้ว่า
Ut = 1/2(P+dP)(Δ+dΔ)
Ut = 1/2(P)(Δ)+1/2(P)(dΔ)+1/2(Δ)(dP)+1/2(dP)(dΔ)
Ut = 1/2(P)(Δ)+1/2(P)(dΔ)+1/2(Δ)(dP)+0
Ut = 1/2(P)(Δ)+1/2(P)(dΔ)+1/2(Δ)(dP) …สมการที่ 4
ทำการแทนให้สมการที่ 3 = สมการที่ 4 จะได้ว่า
½(P)(Δ)+ (P)(dΔ) = 1/2(P)(Δ)+1/2(P)(dΔ)+1/2(Δ)(dP)
(P)(dΔ)-1/2(P)(dΔ) = 1/2(P)(Δ)+1/2(Δ)(dP)-1/2(P)(Δ)
1/2(P)(dΔ) = 1/2(Δ)(dP)
(P)(dΔ) = (Δ)(dP) …สมการที่ 5
จากนั้นเราก็จะแทนสมการที่ 5 ลงในสมการที่ 2 จะได้ว่า
dU = (P)(dΔ) = (Δ)(dP)
Δ = dU/dP = ∂U/∂P …สมการที่ 6
ในทำนองเดียวกันนะครับ ถ้าหากเราต้องการที่จะหาค่าการเสียรูปในรูปแบบของมุมหมุน (ROTATION) ณ ตำแหน่งนี้ เราก็แค่เพียงทำการแทนด้วยค่าโมเมนต์ M กระทำที่ตำแหน่งนี้ ซึ่งก็จะสามารถพิสูจน์ได้ว่า
θ = dU/dM
θ = ∂U/∂M …สมการที่ 7
โดยสาเหตุที่เราใช้เครื่องหมาย PARTIAL DIFFERENIATE แทนที่จะใช้เครื่องหมาย DIFFERENTIATE ไปเลยนั้นก็เป็นเพราะว่าในขั้นตอนการ DIFFERENTIATE นี้เป็นการ PARTIAL DERIVATIVE พจน์ดังกล่าวนี้นั่นเองนะครับ
เอาละครับในครั้งต่อไปเราจะมาเรียนรู้วิธีในการแทนค่าสมการที่เราทราบที่มาที่ไปแล้วในครั้งนี้ในการหาค่าการเสียรูปต่างๆ ของโครงสร้างกันนะครับ ว่ามีรูปแบบสมการเป็นอย่างไร แทนค่าอย่างไร และมีวิธีการพิจารณาไปปรับใช้กับโครงสร้างกันอย่างไร หากเพื่อนๆ ท่านใดที่มีความสนใจในหัวข้อๆ นี้เป็นพิเศษก็สามารถที่จะติดตามอ่านบทความเรื่องนี้ของผมได้ในสัปดาห์หน้านะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#การเตรียมตัวสอบเพื่อที่จะได้ใบประกอบวิชาชีพวิศวกรโยธา
#พิสูจน์ที่มาที่ไปของสมการทางคณิตศาสตร์ที่ว่าด้วยเรื่องหลักการของพลังงาน
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com