สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
วันนี้ผมจะขออนุญาตมาตอบคำถามให้แก่เพื่อนของผมท่านหนึ่งบนเฟซบุ้คแห่งนี้ที่เพื่อนท่านนี้ได้หลังไมค์มาให้ผมช่วยอธิบายถึงค่าโมดูลัสของแรงเฉือน (SHEAR MODULUS) หรือค่าโมดูลัสของความคงรูป (MODULUS OF RIGIDITY) ที่เรานิยมเขียนแทนด้วยค่า G นั่นเองครับ
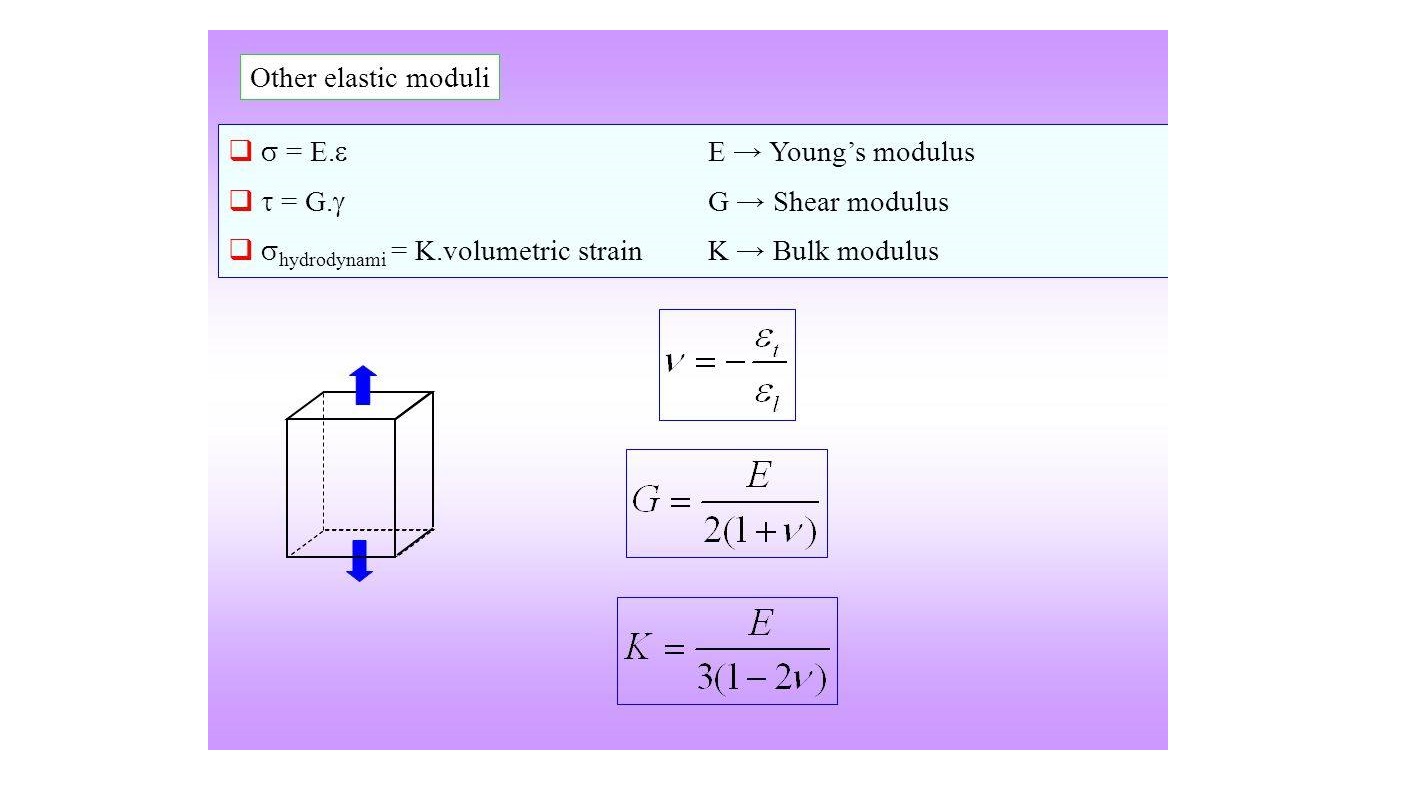
ค่าๆ นี้ถือเป็นปริมาณที่มีประโยชน์มากค่าหนึ่งในทางกลสาสตร์ของวัสดุ ซึ่งชื่อของมันก็ชัดเจนอยู่แล้วนะครับว่าหากวัสดุใดที่มีคุณสมบัติค่าๆ นี้ที่สูง ก็ย่อมที่จะมีค่าการต้านทานต่อแรงเฉือนหรือมีคุณสมบัติทางด้านความคงรูปที่สูงตามไปด้วย
โดยเราจะสามารถทำการทดสอบหาค่านี้ได้โดยสมมติฐานที่ว่าวัสดุนั้นมีการเสียรูปเป็นไปตามกฎของฮุค (HOOK’S LAW) โดยค่าที่จะนำมาใช้พิจารณาในการคำนวณค่าๆ นี้จะต้องเป็นค่าความเค้นและความเครียดที่อยู่ในช่วงเชิงเส้นเท่านั้น
เราสามารถที่จะให้นิยามค่าโมดูลัสของแรงเฉือน (SHEAR MODULUS) หรือค่า โมดูลัสของความคงรูป (MODULUS OF RIGIDITY) ได้จากอัตราส่วนระหว่างค่าความเค้นเชิงเฉือนเชิงเส้น (LINEAR SHEAR STRESS) ต่อ ค่าความเครียดเชิงเฉือนเชิงเส้น (LINEAR SHEAR STRAIN) ซึ่งจะละม้ายคล้ายคลึงกับหลักการในการคำนวณหาค่าโมดูลัสของความยืดหยุ่น (MODULUS OF ELASTICITY) ที่หาได้จากอัตราส่วนระหว่างค่าความเค้นตั้งฉากเชิงเส้น (LINEAR NORMAL STRESS) ต่อ ค่าความเครียดตั้งฉากเชิงเส้น (LINEAR NORMAL STRAIN) กล่าวคือหาก
ค่าความเค้นตั้งฉากเชิงเส้นเท่ากับ σ
ค่าความเครียดตั้งฉากเชิงเส้นเท่ากับ εn
ค่าความเค้นเฉือนเชิงเส้นเท่ากับ S
ค่าความเครียดเฉือนเชิงเส้นเท่ากับ εs
ดังนั้นค่า
E = σ/εn
และค่า
G = S/εs
หรือเราอาจใช้ความสัมพันธ์ระหว่างความเค้นและความเครียดตามกฎของฮุคหาค่า G นี้ได้ตามรูปที่ผมแนบมาด้วยก็ได้ครับ
ในโอกาสหน้าไปผมจะพยายามหาและนำ ตย ในการนำค่า G นี้ไปใช้ในการคำนวณทางด้านกลศาสตร์แก่เพื่อนๆ ได้ดูกันต่อไปนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากพี่แขก และ เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่
ADMIN JAMES DEAN