สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
วันนี้ผมจะมาต่อในเรื่องที่ผมยังค้างเพื่อนๆ เอาไว้กันนะครับ โดยวันนี้ผมจะมาอธิบายเรื่องการคำนวณค่าโมเมนต์ความเฉื่อยประสิทธิผลเมื่อหน้าตัด คสล ของเรานั้นเป็น CRACKED SECTION กัน
มาตรฐาน ACI ได้กำหนดไว้ว่าหากจะทำการคำนวณหาค่าการโก่งตัวในโครงสร้างรับแรงดัดที่เสริมเหล็กทางเดียว
เราจำเป็นจะต้องนำผลของ 2 ส่วนมาคิด คือ
(1) การโก่งตัวแบบทันทีทันใด
(2) การโก่งตัวที่เพิ่มขึ้นตามกาลเวลา
1. การโก่งตัวแบบทันทีทันใด
ในคำนวณหาค่าการโก่งตัวในทันทีทันใดนั้นเราสามารถที่จะใช้ทฤษฎีอิลาสติกในการวิเคราะห์โครงสร้างได้ และ อย่างที่ผมเรียนไปในโพสต์ก่อนหน้านี้ถึงเรื่องหากมีความจำเป็นที่เราจะต้องทำการตรวจสอบค่าการโก่งตัวของโครงสร้าง เราจะต้องสามารถคำนวณหาค่าโมเมนต์ความเฉือยประสิทธิผล หรือ ค่า I eff ของหน้าตัด คสล ออกมาให้ได้ โดยการคำนวณค่า I eff นั้นหาได้จากสมการ
I eff = (Mcr/Ma)^(3) Ig + [ 1 – (Mcr/Ma)^(3) ] I cr
ซึ่งไม่ว่าหน้าตัดของเราจะมีการเสริมเหล็กอย่างไร หรือ รับโมเมนต์ดัดอย่างไรก็ตามค่า I eff ก็จะมีค่าน้อยกว่าค่า Ig เสมอนะครับ
โดยปัจจัยสำคัญที่เกี่ยวข้องในการคำนวณสมการข้างต้นนั้นจะประกอบไปด้วย
-1 ค่าโมดูลัสความเฉื่อยแบบไม่แตกร้าว หรือ INERTIA OF UNCRACKED SECTION ที่เราเรียกสั้นๆ ว่าค่า Ig นั้นเอง
-2 ค่าโมดูลัสความเฉื่อยแบบแตกร้าว หรือ INERTIA OF CRACKED SECTION ที่เราเรียกสั้นๆ ว่าค่า I cr นั้นเอง
-3 ค่าโมดูลัสการแตกร้าว หรือ MODULUS OF RUPTURE ซึ่งจะเกี่ยวพันโดยตรงกับวัสุดคอนกรีต เราทราบกันดีว่ากำลังรับแรงดึงของคอนกรีตนั้นจะเฉลี่ยอยุ่ที่แค่ 10% ของกำลังอัด ดังนั้นยิ่งคอนกรีตมีค่ากำลังรับแรงอัดที่มาก ก็จะยิ่งมีค่าๆ นี้ที่สูงตามไปด้วย ดังนั้นหากใครจะพูดว่าใช้ค่ากำลังรับแรงอัดในคอนกรีตต่ำๆ ในการออกแบบก็ได้ ผมไม่เห็นด้วยนะครับ เพราะกำลังของคอนกรีตจะส่งผลต่อปัจจัยอื่นๆ อีกมาก เช่น ความคงทน หรือ DURABILITY ของโครงสร้าง ความสามารถในการใช้งานที่ดี หรือ SERVICEABILITY ของโครงสร้าง เป็นต้น ซึ่งค่าโมดูลัสการแตกร้าวสามารถหาได้จากสมการ
fr = 2 √fc’
สุดท้ายแล้วเราจะนำค่าๆ นี้ไปเพื่อคำนวรหาค่า Mcr ต่อนั่นเองครับ
-4 ค่าโมดูลสัสยืดหยุ่นของคอกนรีต ซึ่งข้อนี้จะคล้ายๆ กันกับข้อ (3) คือ ค่าโมดูลัสยืดหยุ่นของคอนกรีตจะเป็นฟังก์ชั่นตรงกับค่ากำลังรับแรงอัดของคอนกรีต ซึ่งค่าโมดูลัสยืดหยุ่นของคอนกรีตสามารถหาได้จากสมการ
Ec = 15100 √fc’
-5 ค่าโมเมนต์ดัดใช้งาน หรือค่า Ma ซึ่งค่าๆ นี้จะเป็นตัวแปรสำคัญในการวิเคราห์ค่าการฌก่งตัวในโครงสร้าง คสล เลยนะครับ กล่าวคือ ยิ่งหน้าตัดต้องรับโมเมนต์ดัดใช้งานที่มาก ก็จะยิ่งทำให้ค่าโมดูลัสความเฉื่อยประสิทธิผลของหน้าตัดนั้นมีค่าน้อยลงไปเป็นสัดส่วนโดยตรงต่อค่าๆ นี้ครับ
2. การโก่งตัวที่เพิ่มขึ้นตามกาลเวลา
โดยการโก่งตัวที่เพิ่มขึ้นตามกาลเวลานั้นจะขึ้นอยู่กับความล้าและการหดตัวที่เกิดขึ้นในวัสดุคอนกรีตเป็นหลัก
ปล ค่าๆ นี้จะขึ้นกับตัววัสดุคอนกรีตเป็นหลักเช่นเดียวกันกับที่ผมเคยอธิบายไปก่อนหน้านี้ว่าเหตุใดคุณภาพของคอนกรีตถึงมีความสำคัญมากๆ ในงานก่อสร้าง
ดังนั้นค่าตัวคูณประกอบที่สำคัญก็คือค่าตัวคูณประกอบเนื่องจากการล้า หรือ CREEP FACTOR หรือ ที่เราเรียกสั้นๆ ว่าค่า λ โดยค่าๆ นี้หาได้จาก
λ = ξ / (1 + 50p’)
(หากสังเกตดีๆ จะพบว่าค่าๆ นี้จะขึ้นกับอัตราส่วนการเสริมเหล็กบริเวณที่รับแรงอัดในหน้าตัด หรือ p’ ถึงแม้ว่าหน้าตัดจะไม่ต้องการเหล็กเสริมชนิดนี้ในการเสริมเหล็กในหน้าตัดเลยก็ตามนะครับ)
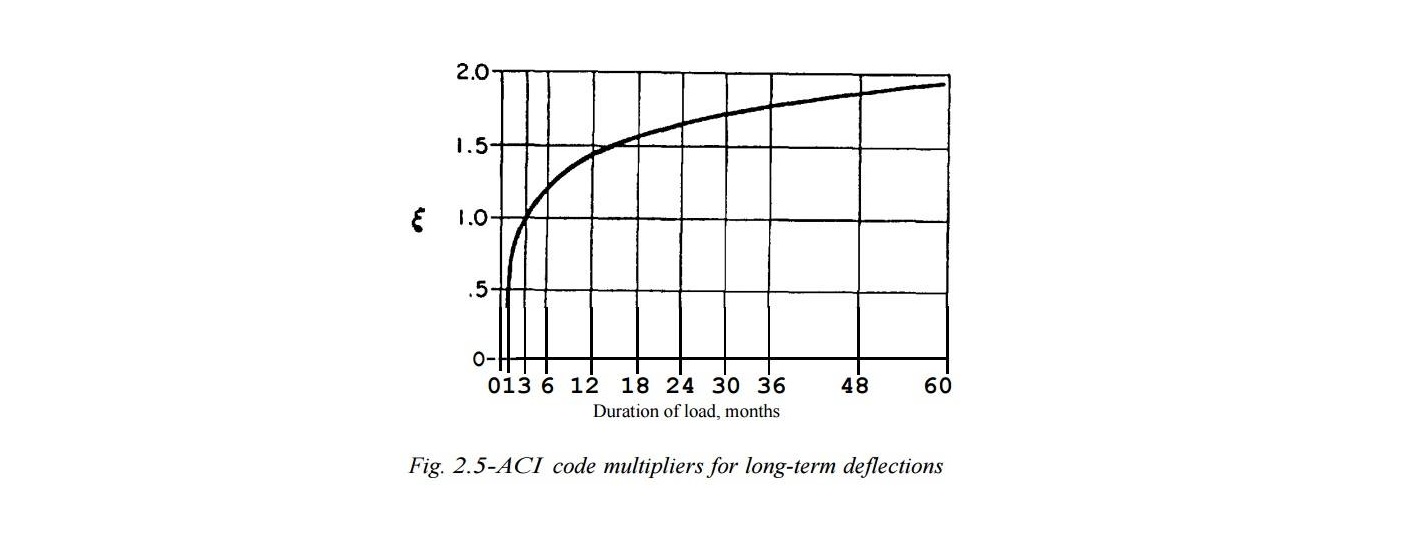
ค่าตัวคูณประกอบอีกตัวหนึ่งที่ถือว่ามีความสำคัญก็คือ ค่าตัวคูณประกอบตามกาลเวลาของการคงค้างของ นน หรือ TIME DEPENDENT FACTOR หรือ ที่เราเรียกสั้นๆ ว่าค่า ξ เป็นสำคัญนั่นเอง
นน บรรทุกคงค้างนาน 5 ปี หรือ มากกว่าค่า ξ = 2.0
นน บรรทุกคงค้างนาน 1 ปี หรือ ξ = 1.4
นน บรรทุกคงค้างนาน 1/2 ปี หรือ ξ = 1.2
นน บรรทุกคงค้างนาน 1/4 ปี หรือ ξ = 1.0
จากค่าข้างต้นจะเห็นว่ายิ่ง นน คงค้างบนโครงสร้างมีอยู่นานเท่าใดก็ค่า ξ ก็จะยิ่งเพิ่มขึ้นมากเท่านั้นครับ (ดูรูปประกอบนะครับ)
เนื้อหาในเรื่องนี้ค่อนข้างที่จะยืดยาวและซับซ้อนนะครับ ผมขอเบรคเนื้อหาไว้เพียงเท่านี้ก่อนละกัน เอาเป็นว่าในครั้งต่อไปผมจะขออนุญาตมาต่อในครั้งหน้านะครับ โดยผมคาดหมายว่าจะสามารถแสดง ตย ประกอบด้วยได้ในการอธิบายในครั้งต่อไปนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN