สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
กลับมาพบกันในทุกๆ วันจันทร์แบบนี้อีกครั้งหนึ่งซึ่งผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะพูดคุยกันถึงหัวข้อ “ความรู้ดีๆ เพื่อคุณผู้หญิง” นะครับ
ตามที่ผมได้เรียนเพื่อนๆ ไปเมื่อในสัปดาห์ที่แล้วว่าวันนี้ผมจะขออนุญาตมาพูดถึงเรื่อง สมการค่าแรงอัดวิกฤติของออยเลอร์ กันต่ออีกสักหนึ่งโพสต์เพราะจริงๆ แล้วเรื่องนี้เป็นเรื่องหนึ่งที่มีความสำคัญมากเกี่ยวกับวิชากลศาสตร์ของวัสดุหรือ MECHANICS OF MATERIALS ซึ่งสุดท้ายแล้วเราก็จะต้องนำเอาพื้นฐานของเรื่องๆ นี้ไปต่อยอดในวิชาออกแบบต่างๆ อีกมากมายเลย เช่น การออกแบบโครงสร้างคอนกรีตเสริมเหล็ก หรือ STRUCTURAL CONCRETE DESIGN การออกแบบโครงสร้างเหล็กรูปพรรณ หรือ STRUCTURAL STEEL DESIGN การออกแบบโครงสร้างไม้ หรือ STRUCTURAL TIMBER DESIGN เป็นต้นนะครับ
ก่อนอื่นเรามาทบทวนเนื้อหาเมื่อในสัปดาห์ที่แล้วกันสักนิดที่ผมได้พาเพื่อนๆ ไปรับชมเป็น รูปแบบของการเสียรูปเนื่องจากการโก่งเดาะ หรือ ที่พวกเรานิยมเรียกชื่อนี้ว่า BUCKLING SHAPE ของโครงสร้างเมื่อต้องทำหน้าที่ในการรับแรงอัด ซึ่งก็จะเห็นได้ว่าเมื่อลักษณะของจุดรองรับของโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดนั้นมีความแตกต่างกันก็จะทำให้มีรูปแบบของการเสียรูปที่มีความแตกต่างกันตามไปด้วย ซึ่งหากเพื่อนๆ สังเกตดูดีๆ ก็จะพบว่าเดิมทีนั้นโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดนั้นจะมีค่าขนาดของความยาวของชิ้นส่วนเท่าๆ กันซึ่งจะมีค่าเท่ากับ L ในที่สุดแล้วเมื่อเกิดการเสียรูปเนื่องจากการโก่งเดาะขึ้นในโครงสร้างค่าของความยาวประสิทธิผลของโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดนั้นก็จะมีค่าที่เปลี่ยนไปและมีความแตกต่างกันด้วย เช่น สำหรับโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดที่มีลักษณะของจุดรองรับเป็นแบบยึดแน่นทั้ง 2 ข้าง ก็จะมีค่าความยาวประสิทธิผลจากเดิมทีมีค่าเท่ากับ L ลดลงเหลือเพียงแค่ 0.50L ในทางกลับกันหากเป็นโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดที่มีลักษณะของจุดรองรับเป็นแบบยึดแน่น 1 ข้างและอีกข้างนั้นเป็นแบบปล่อยอิสระ ก็จะมีค่าความยาวประสิทธิผลจากเดิมทีมีค่าเท่ากับ L เพิ่มขึ้นเป็น 2L เป็นต้นนะครับ
ซึ่งจริงๆ แล้วค่า K ที่เราคำนวณออกมาได้นี้จะได้มาจากการถอดรากที่สองของส่วนกลับของ ค่าตัวคูณปรับแก้ลักษณะของจุดรองรับของโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัด หรือค่า n หรือหากจะเขียนให้อยู่ในรูปสมการก็อาจจะเขียนอธิบายความสัมพันธ์ระหว่างค่า K และ n ได้ว่า
K = √(1/n) (EQ.1)
ทั้งนี้เป็นเพราะว่าค่า n ข้างต้นนี้จะติดมากับ สมการค่าแรงอัดวิกฤติของออยเลอร์ หรือ EULER’S CRITICAL COMPRESSION LOAD หรือ ที่พวกเรานิยมเรียกชื่อนี้ว่า Pcr ซึ่งก็จะสามารถทำการคำนวณออกมาได้โดยผ่านกระบวนการๆ แก้ สมการเชิงอนุพันธ์ หรือ DIFFERENTIAL EQUATION โดยที่จะมีหน้าตาของสมการดังนี้
Pcr = n×π^(2)×E×I/L^(2) (EQ.2)
โดยที่ค่า n คือ ค่าตัวคูณปรับแก้ลักษณะของจุดรองรับของโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัด ส่วนค่า E ก็คือ ค่าโมดูลัสยืดหยุ่นของวัสดุที่ใช้ในการก่อสร้าง หรือ ELASTIC MODULUS สำหรับค่า I ก็คือ ค่าโมเมนต์ความเฉื่อยของหน้าตัดของชิ้นส่วนโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัด หรือ MOMENT OF INERTIA และสุดท้ายก็คือค่า L คือ ความยาวจริงๆ ของชิ้นส่วนโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัดครับ
ทั้งนี้หากผมทำการจัดรูป EQ.1 ใหม่ ก็จะได้ความสัมพันธ์ระหว่างค่า K และค่า n ออกมาดังสมการต่อไปนี้
K = √(1/ n)
K^(2) = √(1/n)^(2)
K^(2) = 1/n
n = 1/K^(2)(EQ.3)
ดังนั้นหากผมทำการแทนค่า EQ.3 ลงไปใน EQ.2 เราก็จะได้สมการค่าแรงอัดวิกฤติของออยเลอร์ใหม่ดังต่อไปนี้
Pcr = n×π^(2)×E×I/L^(2)
Pcr = [1/K^(2)]×π^(2)×E×I/L^(2)
Pcr = π^(2)×E×I/[K^(2)×L^(2)]
Pcr = π^(2)×E×I/[K×L]^(2)(EQ.4)
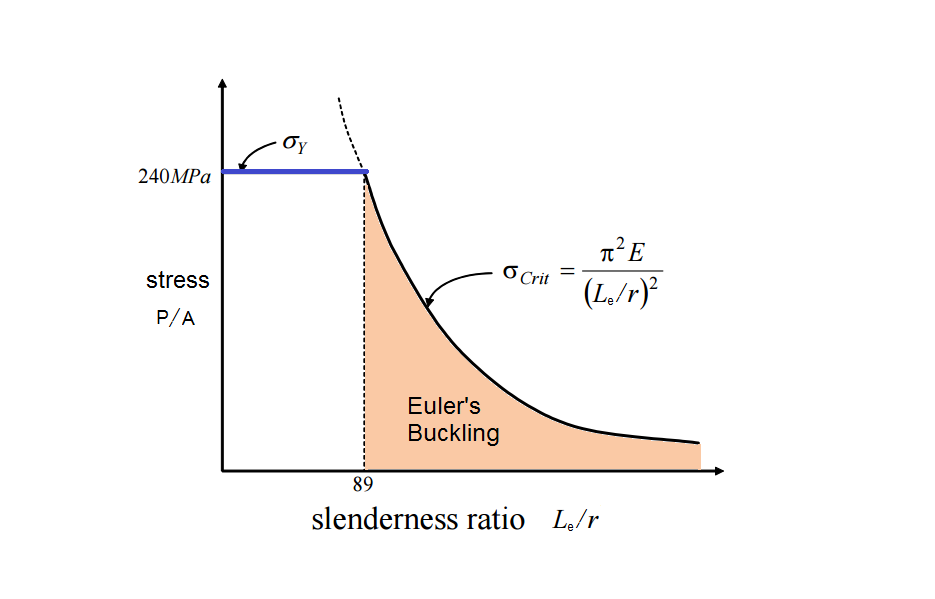
เพื่อนๆ จะเห็นได้จาก EQ.4 ว่าสุดท้ายแล้วค่า K นั้นจะมีผลโดยตรงต่อสมการค่าแรงอัดวิกฤติของออยเลอร์ ทั้งนี้หากเราให้ทุกๆ พารามิเตอร์ภายในสมการๆ นี้มีค่าที่คงที่ทั้งหมดและจะเปลี่ยนไปเฉพาะแค่ค่า K เท่านั้น ดังนั้นยิ่งค่า K นั้นมีค่าที่น้อยเท่าใด ก็จะยิ่งทำให้ผลของ Pcr ที่ได้จากการคำนวณจากสมการค่าแรงอัดวิกฤติของออยเลอร์นั้นมีค่าที่ยิ่งสูงขึ้น ซึ่งเอาเข้าจริงๆ แล้วเรายังสามารถที่จะทำการเปลี่ยนให้ค่าที่คำนวณออกมาได้สมการค่าแรงอัดวิกฤติของออยเลอร์นี้ให้เป็นเทอมอื่นๆ ได้อีก เช่น สมการค่าหน่วยแรงอัดวิกฤติของออยเลอร์ หรือ Fcr เป็นต้น ซึ่งหากเราดูรูปประกอบในโพสต์ๆ นี้ก็จะเห็นได้ว่าเป็นรูปแผนภูมิที่แสดงถึงความสัมพันธ์ระหว่าง ค่าอัตราส่วนความชะลูด หรือ SLENDERNESS RATIO ที่อยู่ในแกน X กับ ค่าของแรงเค้นของชิ้นส่วนโครงสร้างเหล็กรูปพรรณ ที่อยู่ในแกน Y ซึ่งก็จะเห็นได้ว่าจะมีขีดจำกัดๆ หนึ่งที่จะเป็นเส้นที่แบ่งระหว่างการที่ค่าของแรงเค้นของชิ้นส่วนโครงสร้างเหล็กรูปพรรณนั้นจะมีค่าที่คงที่ซึ่งในกรณีของรูปๆ นี้ก็คือที่ค่าอัตราส่วนความชะลูดเท่ากับ 89 โดยหากเมื่อใดที่ค่าอัตราส่วนความชะลูดนั้นมีค่าที่สูงกว่าค่าๆ นี้แล้ว ค่าของแรงเค้นของชิ้นส่วนโครงสร้างเหล็กรูปพรรณนั้นก็จะมีค่าที่ค่อยๆ ลดลงไปขึ้นอยู่กับค่าอัตราส่วนความชะลูดของชิ้นส่วนของโครงสร้าง โดยที่ค่าทั้งสองนี้จะมีความสัมพันธ์ซึ่งกันและกันเป็นแบบไม่เชิงเส้น พูดง่ายๆ ก็คือ ยิ่งอัตราส่วนความชะลูดมีค่าที่มากเท่าใด ก็จะส่งผลทำให้แล้วค่าของแรงเค้นของชิ้นส่วนโครงสร้างเหล็กรูปพรรณนั้นมีค่าน้อยลงไปมากเท่านั้นนั่นเองครับ
ผมหวังว่าวันนี้เพื่อนๆ น่าที่จะมีความรู้และความเข้าใจ รวมถึงทราบถึงความสำคัญเกี่ยวกับเรื่องค่า K นี้กันบ้างแล้ว เอาไว้ในการโพสต์ครั้งหน้าผมจะขออนุญาตมาทำการยกตัวอย่างถึงเรื่องการคำนวณเกี่ยวกับเรื่องๆ นี้กันต่ออีกสักหนึ่งโพสต์ก็แล้วกันนะ หากเพื่อนๆ ท่านใดที่อาจจะมีความสนใจในหัวข้อๆ นี้เป็นพิเศษ ก็สามารถที่จะติดตามรับชมและอ่านบทความนี้ของผมได้ในโพสต์ของสัปดาห์หน้านะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำถามในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันจันทร์
#ความรู้ที่มีประโยชน์เพื่อคุณผู้หญิง
#ความสำคัญของค่าตัวคูณเพื่อหาความยาวประสิทธิผลในโครงสร้างที่ต้องทำหน้าที่ในการรับแรงอัด
ADMIN JAMES DEAN
Bhumisiam (ภูมิสยาม)
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปันไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service)
บริษัท ภูมิสยาม ซัพพลาย จำกัด ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม เสาเข็มสปันไมโครไพล์ Spun Micro Pile และเสาเข็มไอไมโครไพล์ I Micropile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กแบบแรงเหวี่ยง มอก.397-2562 และมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กอัดแรงหล่อสำเร็จ มอก.396-2549 การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน ทดสอบการรับน้ำหนักโดยวิธี Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
สอบถามเพิ่มเติมได้ 24ชม. ทุกวันค่ะ
☎️ 082-790-1447
☎️ 082-790-1448
☎️ 082-790-1449
☎️ 091-9478-945
☎️ 091-8954-269
📲 https://lin.ee/hum1ua2
📥 https://m.me/bhumisiam