สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
ในวันนี้ผมจะขออนุญาตมาทำการยก ตย ให้แก่เพื่อนๆ ได้ทราบกันถึงวิธีในการคำนวณหาค่า p นี้ในการแทนค่าหาค่า σ max ในโครงสร้างคานรับแรงดัดต่อเนื่องจากโพสต์ของผมเมื่อวันก่อนนะครับ
ผมขอพูดถึงสาเหตุที่ผมทำการหยิบยกเรื่องๆ นี้มาฝากแก่เพื่อนๆ อีกสักครั้งนะครับ เป็นเพราะว่าผมเห็นว่าในหลายๆ ครั้งเพื่อนๆ มักไม่ได้นำความรู้ รวมไปถึงค่าต่างๆ ในหัวข้อนี้ไปใช้ในการวิเคราะห์ความเค้นในคานกันสักเท่าใดเลยนะครับ เพราะ เพื่อนหลายๆ คนมักจะมีความเข้าใจว่าในการหาค่าความเค้นในคานเราจำเป็นที่จะต้องทำการวิเคราะห์หาแรงปฏิกิริยาของจุดรองรับ หาค่าโมเมนต์ดัด และ จากนั้นเราจึงจะสามารถทราบได้ว่าคานนั้นจะมีความเค้นดัดเกิดขึ้นในหน้าตัดเป็นค่าเท่าใด เอาเป็นว่าวันนี้ผมจะมาให้คำแนะนำกับเพื่อนๆ ก็แล้วกันนะครับว่าการหาความเค้นดัดในคานนั้นเราไม่จำเป็นที่จะต้องทำเช่นนั้นก็ได้นะครับ เรามาเริ่มต้นดูรูปที่ผมแนบมาด้วยประกอบคำอธิบายของผมกันเลยดีกว่านะครับ
โดยผมขอย้อนความถึงโพสต์ที่แล้วของผมก่อนสักเล็กน้อยก็แล้วกันนะครับ หากเพื่อนๆ กลับไปดูจะพบว่าเราสามารถที่จะใช้สมการที่ [13] ในการหาค่า σ max ได้อยู่แล้วนะครับ
σ max = M C / I [13]
และอย่างที่ผมเรียนได้ทำการพิสูจน์ให้เพื่อนๆ ได้รับทราบถึงความสัมพันธ์ระหว่างค่า CURVATURE ของคานว่าจะมีค่าเท่ากับสมการที่ [15]
k = 1 / p [15]
ดังนั้นเราก็จะสามารถคำนวณหาค่า σ max ได้จาก [16] เช่นเดียวกันครับ
σ max = E C k [16]
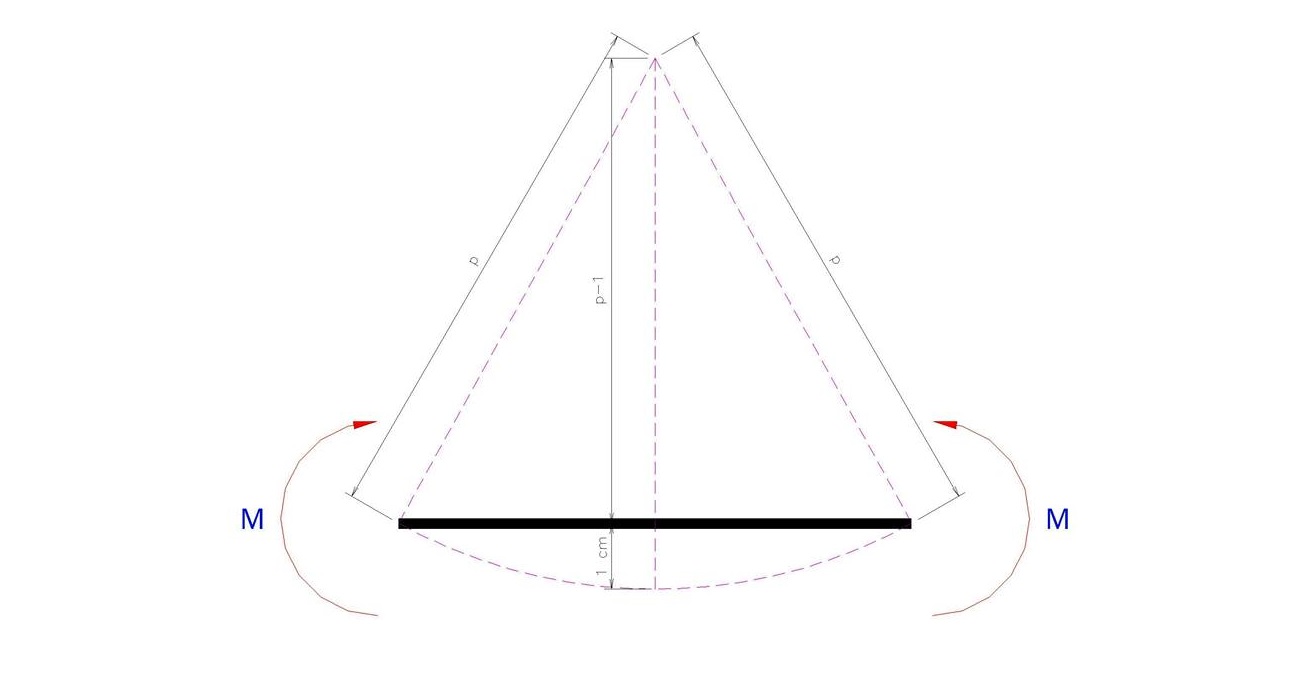
เรามาดู ตย กันเลยดีกว่านะครับ ผมมีคานเหล็กรูปทรงสี่เหลี่ยมตัน ที่มีค่าโมดูลัสยืดหยุ่นเท่ากับ 2×10^(6) ksc มีขนาดความกว้างเท่ากับ 5 cm และ ความลึกเท่ากับ 10 cm โดยที่คานๆ นี้เป็นคานแบบช่วงเดียวอยู่ช่วงหนึ่งที่มีความยาวของคานเท่ากับ 4 m โดยที่เราทราบว่าคานๆ นี้มีการเสียรูปที่กึ่งกลางคานเท่ากับ 1 cm ซึ่งในสถานการณ์จริงๆ นั้นเราไม่ทราบว่าคานๆ นี้ถูกกระทำด้วย นน เท่าใดนะครับ แต่ ผมขอเฉลยไว้ตรงนี้ก็แล้วกันนะครับ เพื่อนๆ จะได้สามารถตรวจคำตอบกันได้ โดยที่คานนี้ถูกกระทำด้วยโมเมนต์ดัด M ที่ปลายของคานที่มีขนาดเท่ากับ 500 kgf-m (ดูรูปประกอบนะครับ) เราจะมาหาค่า σ max ของคานๆ นี้กันนะครับ
จากรูป และ ข้อมูลนะครับ ในการวิเคราะห์หาค่า σ max สำหรับปัญหาที่เราทราบว่าระยะการเสียรูปที่กึ่งกลางคานว่ามีขนาดเท่ากับ 1 cm และ ขนาดความยาวของคานทั้งหมดเท่ากับ 4 m หรือ 400 cm ดังนั้นระยะครึ่งหนึ่งของความยาวจะเท่ากับ 200 cm แล้ว เราก็ไม่มีความจำเป็นที่จะต้องทราบค่า M ที่กระทำที่ปลายของคานเลยนะครับ ก่อนอื่นๆ เราจะอาศัยความสัมพันธ์ของปิทาโกรัสเพื่อหาค่า p เสียก่อนจาก
(p-1)^(2) + 200^(2) = p^(2)
p = 20000.5 cm
ค่า C ของคานรูปตัดสี่เหลี่ยมจะมีค่าเท่ากับ
C = h/2 = 10 / 2 = 5 cm
ค่าโมดูลัสความเฉื่อยของหน้าตัดจะมีค่าเท่ากับ
I = b h^(3) / 12 = (6)(10)^(3)/12 = 500 cm^(4)
จากนั้นเราจะใช้สมการที่ [15] และ [16] ในการคำนวณหาค่า σ max กันนะครับ
k = 1/p = 1/20000.5 = 5×10^(-5) ซม^(-1)
และ
σ max = E C k = 2×10^(6)x5x5x10^(-5) = 500 ksc ◄
เราจะมาลองตรวจคำตอบกันดูนะครับว่าหากเรานำค่า M ที่ผมได้เฉลยไว้ให้เพื่อนๆ เอาไว้มาคำนวณ คำตอบยังจะได้เท่าเดิมอยู่หรือไม่นะครับ ก่อนอื่นเราทราบว่าสมการในการคำนวณหาค่าการเสียรูปที่กึ่งกลางช่วงของคานที่ถูกกระทำด้วย นน M ที่ปลายคานจะมีค่าเท่ากับ
Δ max = M L^(2) / 8EI = 500x100x400^(2) / (8x2x10^(6)x500) = 1 cm
จะเห็นว่าค่า Δ ที่คำนวณออกมาได้จะเท่ากับค่า Δ ที่ผมได้กำหนดไว้ให้ใช้ในการคำนวณปัญหาข้อนี้นะครับ ดังนั้นเราจะอาศัยสมการที่ [13] มาคำนวณหาค่า σ max กันต่อก็แล้วกันนะครับ
σ max = M C / I = 500x100x5 / 500 = 500 ksc ◄
จะเห็นได้ว่าคำตอบของค่า σ max ไม่ว่าเราจะคำนวณด้วยสมการที่ [13] หรือ [16] ก็จะได้คำตอบของค่า σ max ที่เท่าๆ กันนะครับ เป็นเพราะว่าผมได้ทำการพิสูจน์สมการเหล่านี้ให้เพื่อนๆ ได้เห็นแล้วว่าสมการเหล่านี้นั้นมีที่มาที่ไปมาจากหลักการของการคำนวณเดียวกันนั่นเองนะครับ
ดังนั้นในการคำนวณหาค่า σ max ในสถานการณ์จริงๆ นั้นเพื่อนๆ อาจจะสามารถที่จะทำการตรวจสอบวัดค่า Δ max ได้ด้วยสายตา หรือ เครื่องคำนวณต่างๆ เช่น ระดับน้ำ ไม้ระดับ หรือ กล้องระดับ เป็นต้น แต่ การคำนวณว่าคานของเพื่อนๆ นั้นต้องรับค่า M เท่ากับเท่าใดนั้นดูจะทำได้ยากกว่ามากๆ โดยผมคาดหวังว่าหากเพื่อนๆ นำหลักการๆ นี้ของผมไปใช้ก็น่าที่จะเป็นประโยชน์ และ สามารถที่จะใช้ช่วยแก้ปัญหาของเพื่อนๆ ได้นั่นเองนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN