สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
เนื่องจากเมื่อวันก่อนที่แอดมินได้มีโอกาสเขียนบทความให้เพื่อนๆ ได้รู้จักถึงวิธีการออกแบบโครงสร้างเหล็กด้วยวิธีพลาสติกที่ใช้สมรรถนะของโครงสร้างเป็นเกณฑ์ หรือ PBPD (PERFORMANCE BASED PLASTIC DESIGN) ให้เพื่อนๆ ได้รู้จักกันไปในเบื้องต้นแล้วว่า วิธีการออกแบบโครงสร้างเหล็กด้วยวิธีพลาสติกที่ใช้สมรรถนะของโครงสร้างเป็นเกณฑ์ หรือ PERFORMANCE-BASED PLASTIC DESIGN (PBPD) จะประกอบไปด้วยกระบวนการออกแบบขั้นตอนหลักๆ ดังต่อไปนี้ครับ
(1) การกำหนดกลไกการคราก (PRE-SELECTED YIELDING MECHANISM)
(2) การคำนวณหาแรงเฉือนที่ฐานของอาคารสำหรับการออกแบบ (DESIGN BASE SHEAR)
(3) การกระจายแรงเฉือนเป็นแรงกระทำทางด้านข้างแก่อาคาร (DESIGN LATERAL FORCE)
(4) การออกแบบชิ้นส่วนที่ต้องการให้เกิดการครากขึ้นด้วยวิธีวิเคราะห์แบบพลาสติก (DESIGN OF DESIGNATED YIELDING MEMBER)
(5) การออกแบบชิ้นส่วนที่ไม่ต้องการให้เกิดการคราก (DESIGN OF NON-DESIGNATED YIELDING MEMBER)
โดยที่เมื่อวันก่อนแอดมินได้ทำการอธิบายถึงหัวข้อที่ (1) ไปแล้ว ในวันนี้แอดมินจึงจะขอมาอธิบายต่อในหัวข้อที่ (2) กันต่อนะครับ
(2) การคำนวณหาแรงเฉือนที่ฐานของอาคารสำหรับการออกแบบ (DESIGN BASE SHEAR)
แรงเฉือนที่ฐานสำหรับวิธีการออกแบบโครงสร้างเหล็กด้วยวิธีพลาสติกที่ใช้สมรรถนะของโครงสร้างเป็นเกณฑ์สามารถหาได้จากทฤษฎีการเท่ากันของพลังงาน (ENERGY BALANCE CONCEPT) ดังแสดงไว้ในสมการข้างล่างนะครับ
(Ee+Ep) = γE = γ(1/2)(M)(Sv)^(2)
โดยที่
Ee คือ ค่าพลังงานอิลาสติก (ELASTIC ENERGY)
Ep คือ ค่าพลังงานพลาสติก (PLASTIC ENERGY)
M คือ ค่ามวลของทั้งระบบ
Sv คือ ค่าความเร็วตอบสนองเชิงเสปคตรัมสำหรับการออกแบบ
γ คือ ค่าตัวประกอบค่าพลังงาน
เพื่อนๆ สามารถที่จะดูรูป ตย ประกอบได้นะครับ ในรูปจะเป็นแผนภูมิแสดงความสัมพันธ์ระหว่างค่าแรงเฉือนที่ฐาน และค่าการเสียรูปทางด้านข้างของระบบโครงสร้างภายใต้หลักการเท่ากันของพลังงานนั่นเองครับ
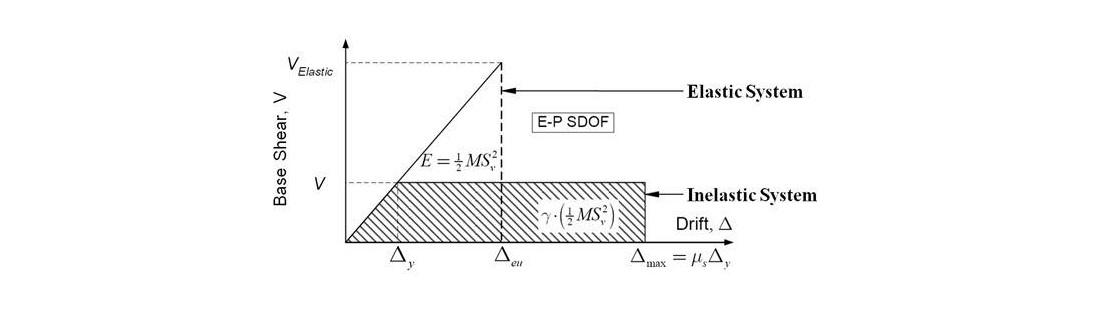
โดยที่ค่าตัวประกอบค่าพลังงาน γ นั้นสามารถหาได้จากสมการที่แสดงครับ
γ = (2μs – 1) / (Rμ)^(2)
โดยที่
γ คือ ค่าตัวประกอบค่าพลังงาน
μs คือ ค่าความเหนียวของโครงสร้าง
Rμ คือ ค่าตัวประกอบปรับลดผลตอบสนองของโครงสร้าง
ค่าพลังงานที่ต้องการของระบบจะสามารถหาได้จากค่าความเร่งตอบสนองเชิงเสปคตรัมสำหรับการออกแบบ (ELASTIC DESIGN SPECTRAL ACCELERATION) ซึ่งมักมีระบุไว้ในข้อกำหนดในการออกแบบ (DESIGN SPECIFICATION) อยู่แล้วครับ ดังนั้นสมการกำลังงาน-พลังงานสามารถเขียนได้ใหม่ตามสมการข้างล่างครับ
(Ee+Ep) = γ(1/2)(M)(Sv)^(2) = γ(1/2)(M)[(Sa)(g)(T/2π)]^(2)
ทั้งนี้ค่าพลังงานอิลาสติก (Ee) สามารถหาได้โดยการสมมุติให้ระบบโครงสร้างเปรียบเสมือนระบบ SINGLE DEGREE OF FREEDOM (SDOF) โดยสามารถหาได้จากสมการข้างล่างครับ
Ee = (1/2)(M)[(g)(V/W)(T/2π)]^(2)
โดยที่
V คือ ค่าแรงเฉือนออกแบบที่ฐาน
W คือ ค่าน้ำหนักที่ใช้คำนวณเกี่ยวกับแผ่นดินไหว (W = Mg)
ค่าแรงเฉือนที่ฐานของอาคารสามารถหาได้จากการแก้ระบบสมการที่กล่าวถึงข้างต้น โดยการหาค่า Ep ซึ่งสัมพันธ์กับค่า V และ การเสียรูปของอาคาร โดยในท้ายที่สุดแล้วค่า V จะมีค่าเท่ากับ
V = (W/2){ -α + SQRT[ α^(2) + 4γ (Sa)^(2) ] }
โดยที่ค่า α คือ ค่าคงที่ไร้มิติ ซึ่งเป็นค่าที่ขึ้นกับค่าสติฟเนสมวลของโครงสร้าง ค่าคุณสมบัติต่างๆ ของรูปแบบการเสียรูป และ ระดับของการเสียรูปทางด้านข้างที่เกิดในสภาวะพลาสติก ดังนั้นเราสามารถที่จะหาค่า α ได้ ทั้งนี้จะขึ้นกับการกำหนดการกระจายตัวของแรงดันทางด้านข้างในขณะทำการออกแบบด้วยนั่นเองครับ
ในวันพรู่งนี้แอดมินจะมาเล่าให้ฟังถึงในหัวข้อที่ (3) (4) และ (5) กันต่อนะครับ อย่างไรต้องขอขอบพระคุณเพื่อนๆ ที่ติดตามและให้ความสนใจอ่านบทความที่แอดมินเขียนมาโดยตลอดนะครับ
ก็หวังเป็นอย่างยิ่งว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากเพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชนต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JD @ ภูมิสยามไมโครไพล์