สวัสดีครับเพื่อนๆ ที่รักทุกๆ ท่าน
สืบเนื่องจากเมื่อวันก่อนที่ผมได้โพสต์แชร์ความรู้และประสบการณ์ในการออกแบบโครงสร้างอาคารสูง (HIGH RISE BUILDING) และ อาคารที่มีช่วงเสาค่อนข้างยาว (LONG SPAN BUILDING) โดยได้แนะนำเพื่อนๆ ว่าในการออกแบบอาคารเหล่านี้ เราควรคำนึงและตรวจสอบค่า BRI หรือค่า BENDING RIGIDITY INDEX ของอาคารด้วยว่าการวางตำแหน่งเสาต่างๆ นั้นวางได้เหมาะสมและมีประสิทธิภาพต่อการรับแรงดัดมากน้อยเพียงใด
(รูปที่ 1)
(รูปที่ 2)
(รูปที่ 3)
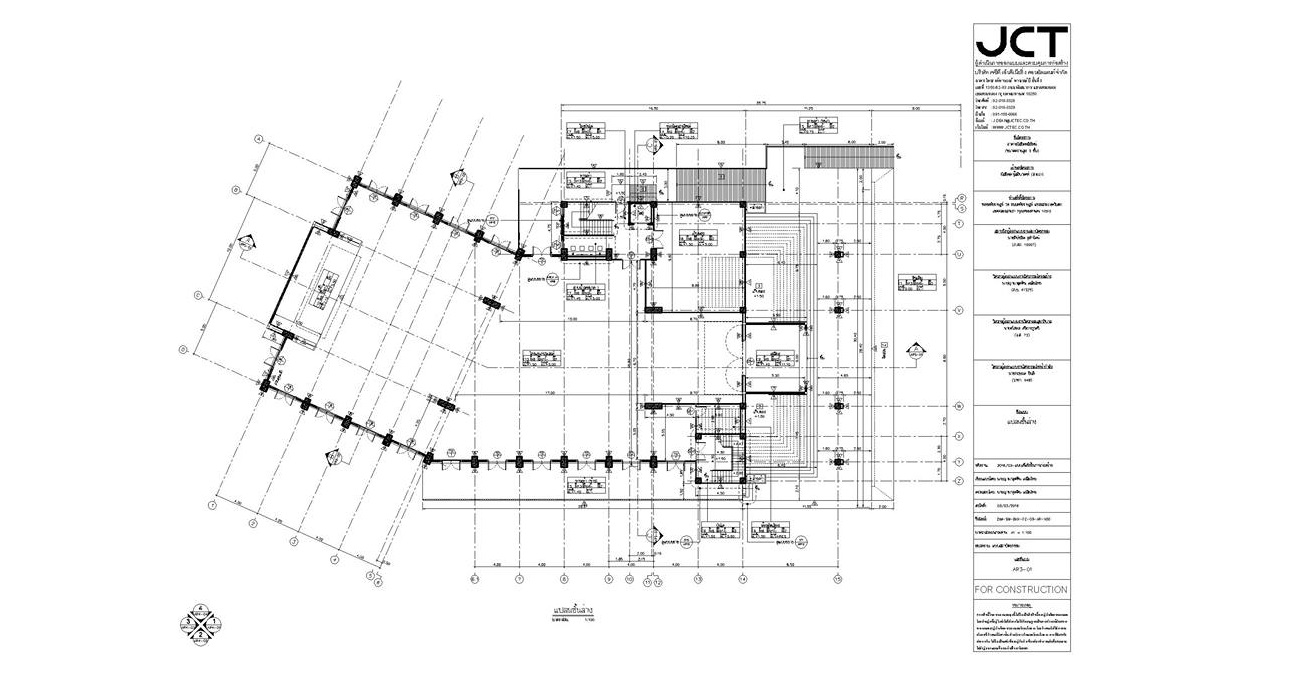
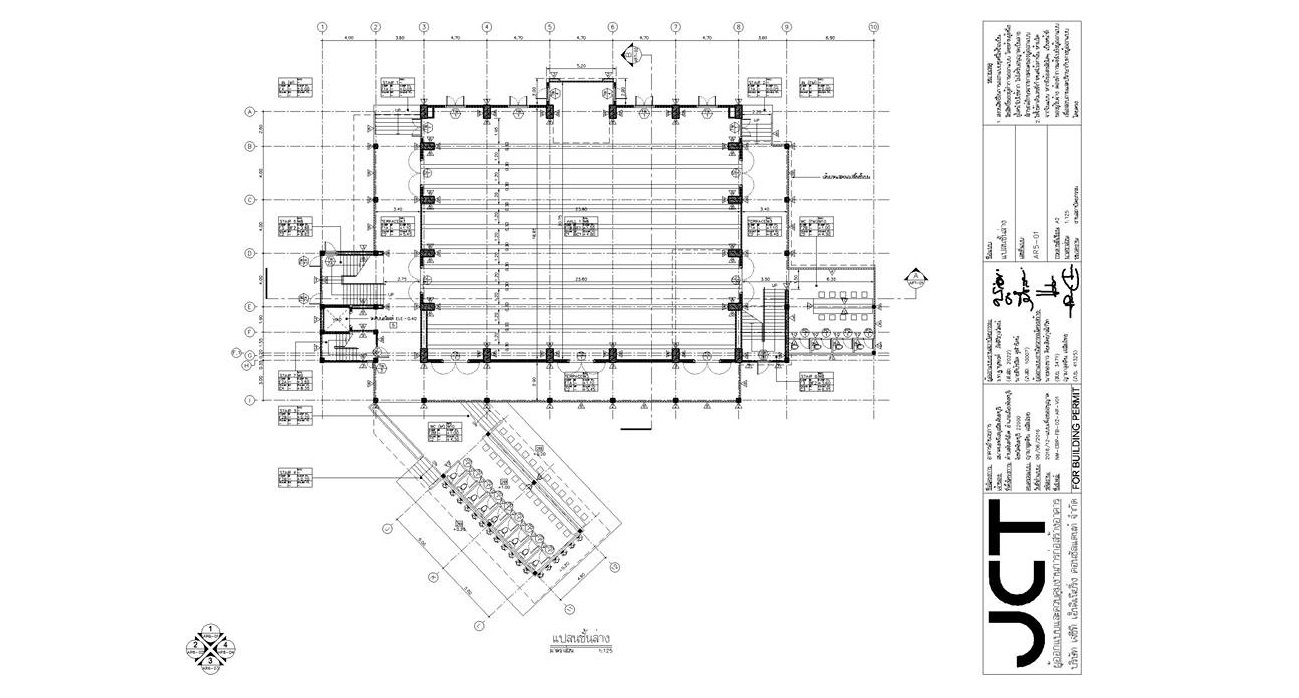
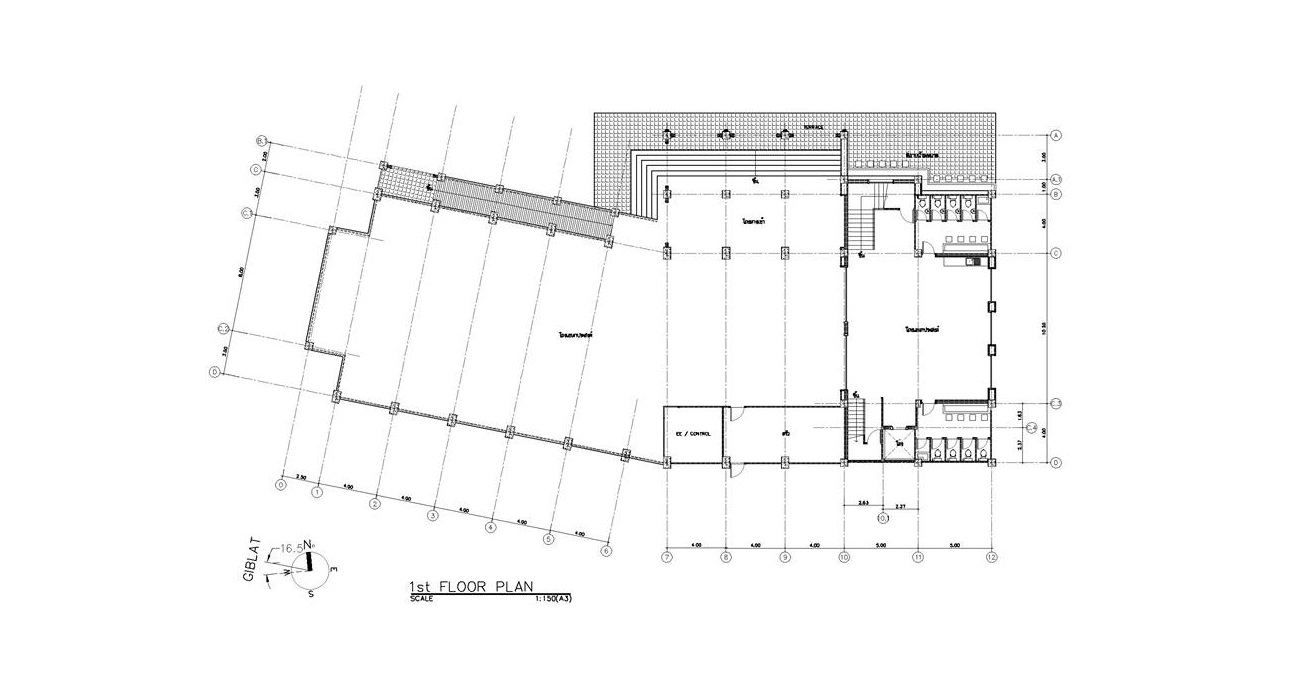
ก่อนอื่นผมอยากจะให้เพื่อนๆ ได้ดูรูปที่ 1 รูปที่ 2 และ รูปที่ 3 ซึ่งเป็นรูปแบบแปลนของอาคารในอดีตที่ผมเคยออกแบบก่อนนะครับ จะเห็นได้ว่าอาคารเหล่านี้เป็นอาคารที่มีลักษณะความยาวช่วงของเสาที่ค่อนข้างยาวมากๆ เวลาที่ทางสถาปนิกออกแบบตำแหน่งเสาต่างๆ มาในแปลนสถาปัตยกรรม ผมก็จะทำการตรวจสอบว่าขนาด จำนวน ตำแหน่งการวาง ของเสาเหล่านี้มีความเหมาะสมเพียงใด โดยหนึ่งในหลายๆ อย่างที่ผมต้องตรวจสอบในฐานะวิศวกรโครงสร้างก็คือค่า BRI นี่เองครับ
พอเมื่อวานผมโพสตืเกี่ยวกับเรื่องๆ นี้ก็มีน้องวิศวกรท่านหนึ่งมีความสนใจในประเด็นดังกล่าว น้องสอบถามมาว่า อยากให้ผมยก ตย การคำนวณค่า BRI นี้ให้ดูเพื่อเป็นวิทยาทานสักหน่อย พออ่านหนังสือทบทวนจากทีไ่ด้เรียนไปวันนี้เสร็จก็เลยคิดว่าจะขอทำ ตย ง่ายๆ เพื่อเป็นวิทยาทานให้แก่เพื่อนๆ ทุกท่านได้ดูกันนะครับ
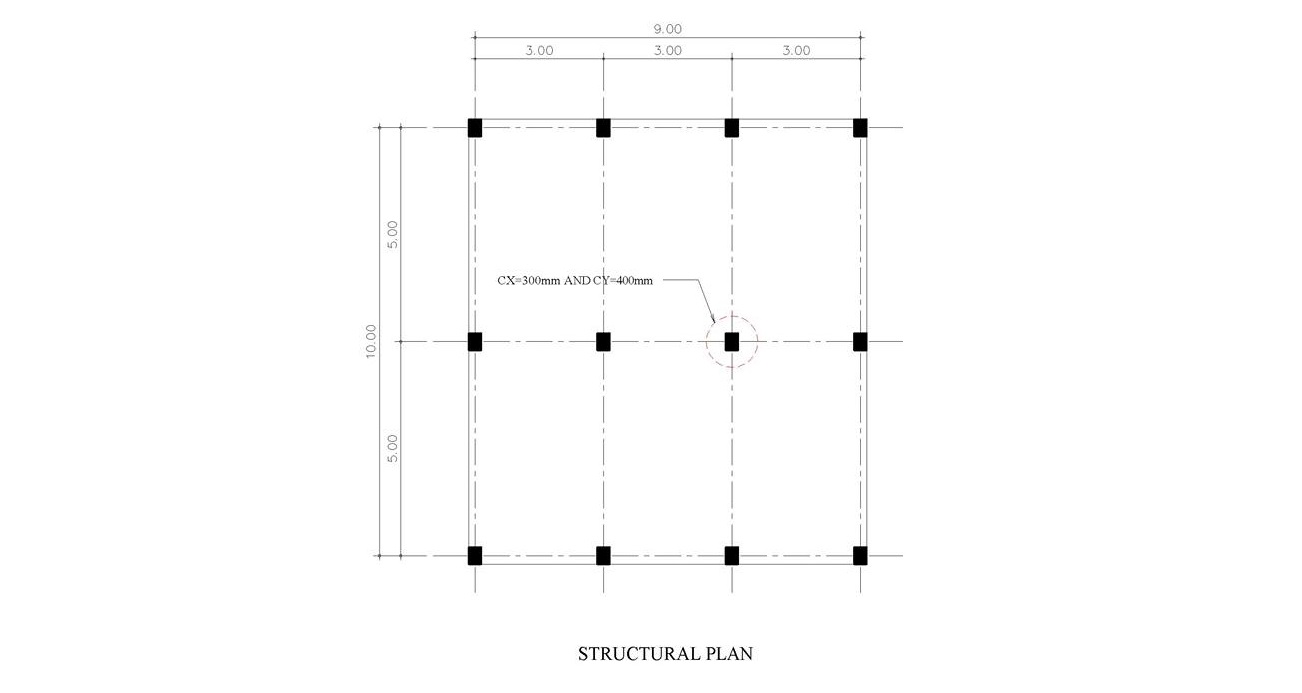
(รูปที่ 4)
ดูรูปที่ 4 นะครับ ในรูปจะเป็นแปลนของอาคารสมมติอาคารแห่งหนึ่ง ในทิศทางขนานแกน X ถูกวางด้วยเสาจำนวน 4 แถว 3 ช่วง ระยะห่างช่วงละ 3 เมตร ทำให้มีขนาดความกว้างของอาคารทั้งหมดเท่ากับ 9 เมตร ในทิศทางขนานแกน Y ถูกวางด้วยเสาจำนวน 3 แถว 2 ช่วง ระยะห่างช่วงละ 5 เมตร ทำให้มีขนาดความกว้างของอาคารทั้งหมดเท่ากับ 10 เมตร ประกอบไปด้วยโครงสร้างเสาทั้งหมด 12 ต้น โดยเสาแต่ละต้นมีขนาดเท่าๆ กัน คือ กว้างขนานทางด้านแกน X เท่ากับ 300 มม และ ยาวขนานทางด้านแกน Y เท่ากับ 400 มม เราจะเริ่มต้นคำนวณค่า พท หน้าตัดทั้งหมดของเสาก่อนนะครับ
เริ่มต้นที่เสาแต่ละต้นก่อนนะครับ
Ag = 30×40 = 1200 cm^(2)
รวมเสาทุกๆ ต้น
∑Ag = 1200×12 = 14,400 cm^(2)
(รูปที่ 5)
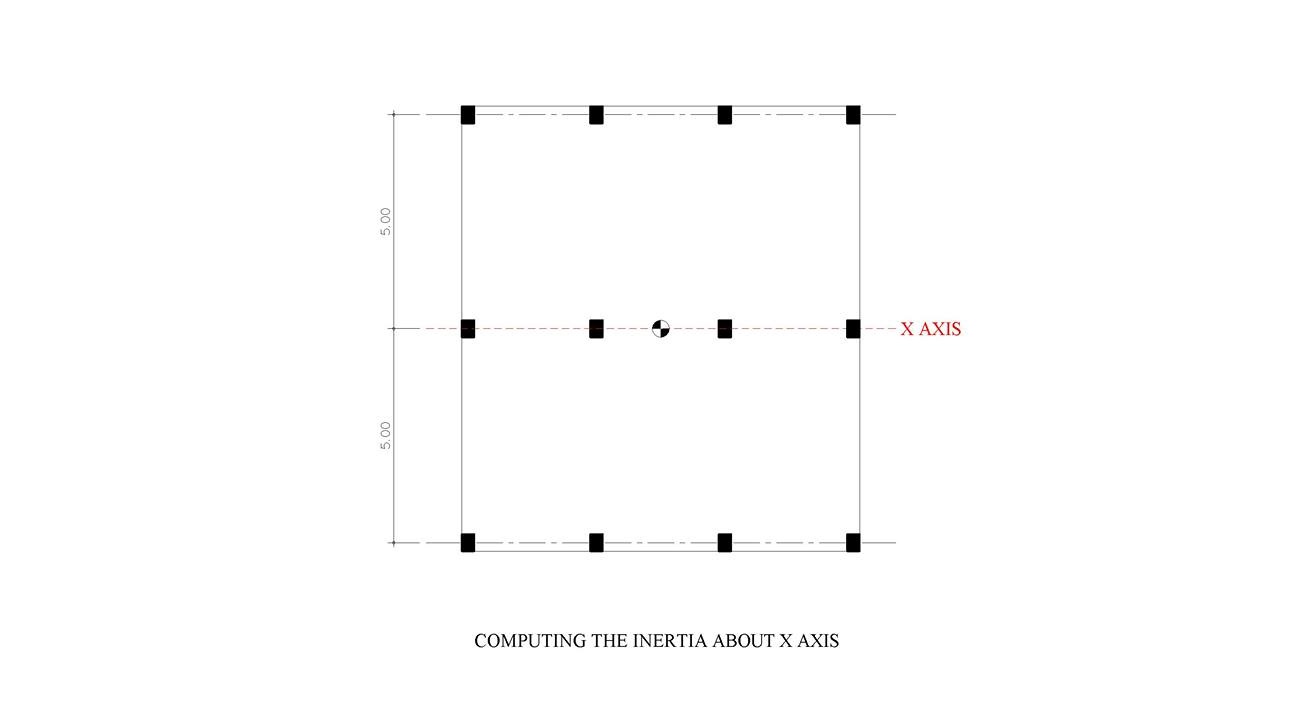
รูปที่ 5 เราจะเริ่มต้นคำนวณค่าต่างๆ รอบแกน X ก่อนนะครับ
เริ่มต้นที่เสาแต่ละต้นก่อนนะครับ
Ix = 30×40^(3)/12 = 160,000 cm^(4)
รวมเสาทุกๆ ต้นรอบแกน X
Ix-x = ∑[Ix + Ag d^(2)]
Ix-x = 12×160,000 + 8×1,200×500^(2)
Ix-x = 2.40×10^(6) cm^(4)
(รูปที่ 6)
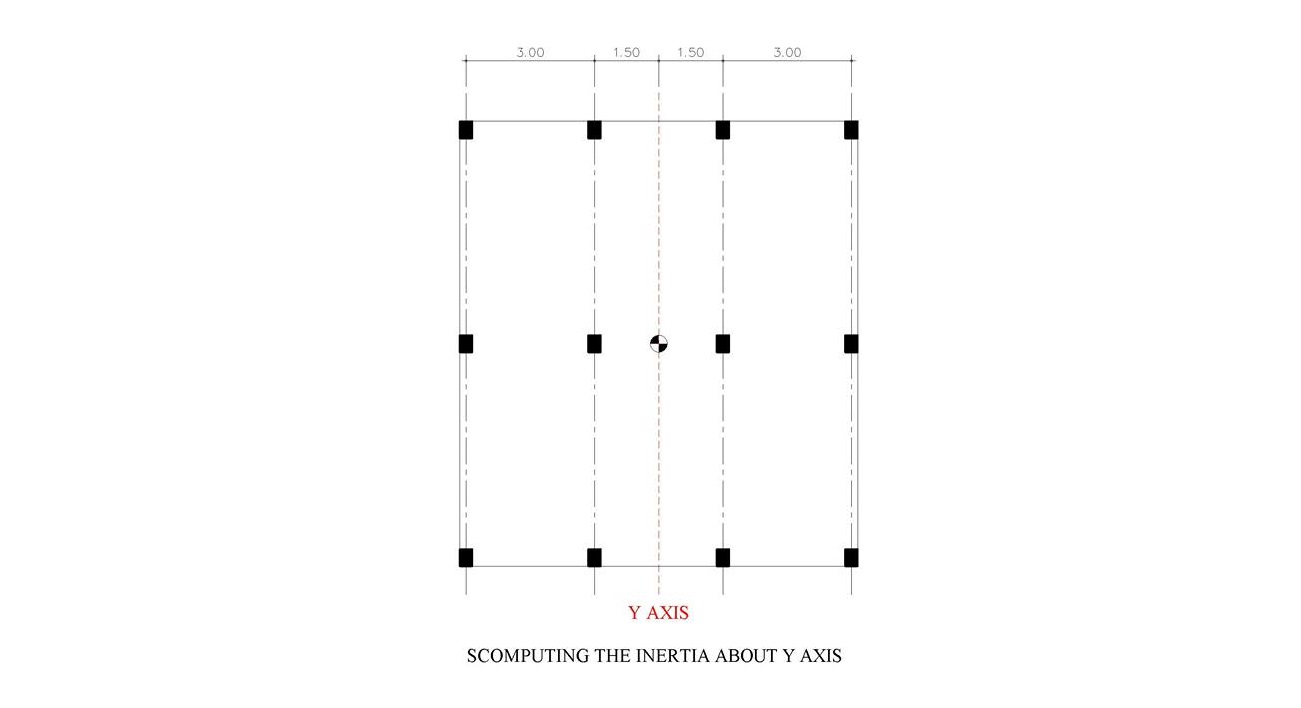
รูปที่ 6 เราจะเริ่มต้นคำนวณค่าต่างๆ รอบแกน Y ต่อนะครับ
เริ่มต้นที่เสาแต่ละต้นก่อนนะครับ
Iy = 40×30^(3)/12 = 90,000 cm^(4)
รวมเสาทุกๆ ต้นรอบแกน X
Iy-y = ∑[Iy + Ag d^(2)]
Iy-y = 12×90,000 + 6×1,200x[150^(2) + 450^(2)]
Iy-y = 1.62×10^(6) cm^(4)
(รูปที่ 7)
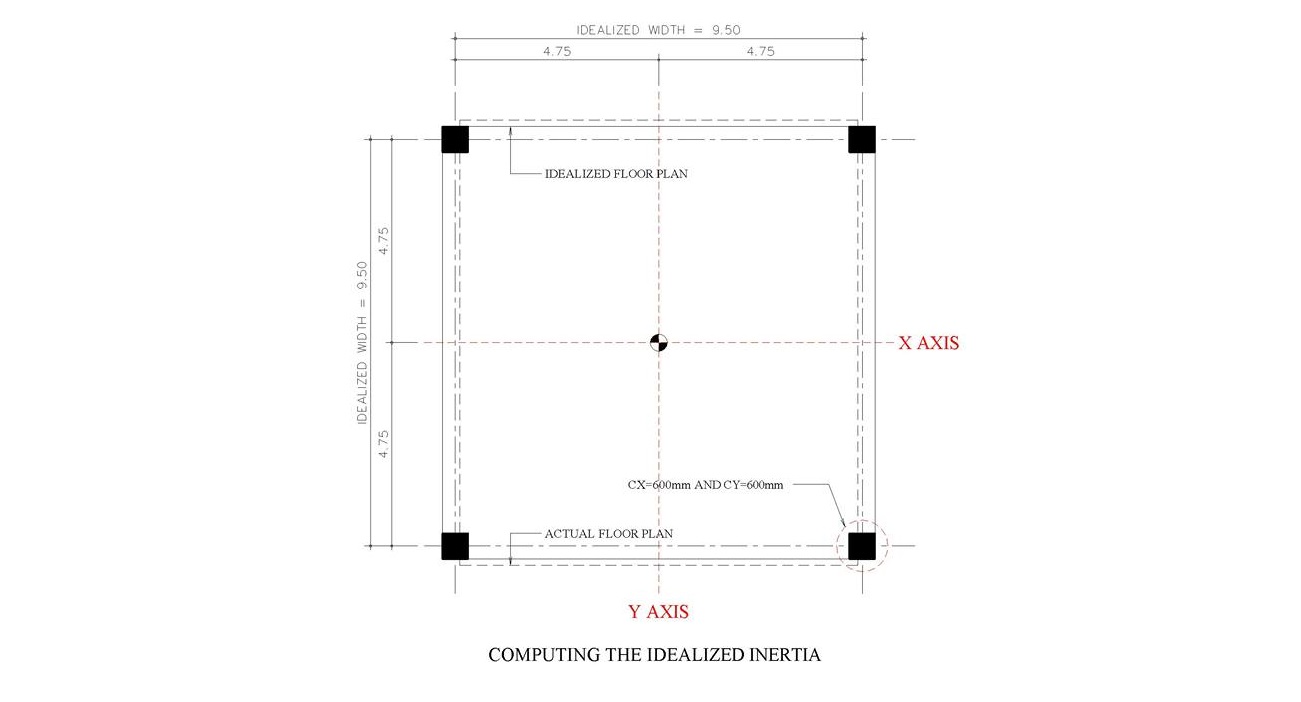
รูปที่ 7 ซึ่งเป็นรูปสุดท้าย เราจะคำนวณค่าที่มากที่สุดกันนะครับ
เราจะคำนวณโดยใช้หลักการคิดให้ พท เป็นสี่เหลี่ยมจตุรัส มีเสาสี่เหลี่ยมจตุรัสวางที่ทั้ง 4 มุม หากดูขนาดของอาคารแล้วพบว่ามีขนาดเท่ากับ 9×10 เมตร ซึ่งจะใกล้เคียงกับสี่เหลี่ยมจตุรัสอยู่แล้ว โดยหากไม่คำนวณเลยก็พอจะคาดเดาได้ว่าค่า BRI ที่คำนวณได้น่าจะมีค่ามากใช้ได้อยู่นั่นเองครับ
เราต้องหาค่าเฉลี่ยในแต่ละด้านก่อนนะครับ ความกว้างเท่ากับ 9 เมตร เราจะปัดขึ้นเป็น 9.5 เมตร ส่วนความยาวเท่ากับ 10 ม เราจะปัดลงเป็น 9.5 เมตร เพียงเท่านี้ก็ได้ขนาดของอาคารเป็นสี่เหลี่ยมจตุรัสเรียบร้อยแล้วครับ
เรามาเริ่มต้นคำนวณหาค่าขนาดของเสารูปทรงสี่เหลี่ยมจตุรสแต่ละต้นก่อนนะครับ
B = √(14,400/4) = 60 cm
ขนาดของเสาแต่ละต้นจะเท่ากับ
Ag = 60^(2) = 3,600 cm^(2)
ค่า INERTIA ของเสาแต่ละต้นจะมีค่าเท่ากับ
I = 60^(4)/12 = 1.08×10^(6) cm^(4)
รวมค่า I ของเสาทั้ง 4 ต้นรอบแกน X และ Y
I = Ix-x = Iy-y = ∑[Ix + Ag d^(2)]
I = Ix-x = Iy-y = 4×1.08×10^(6) + 4×3,600×475^(2)
I = Ix-x = Iy-y = 3.25×10^(6) cm^(4)
ต่อมาเราจะมาคำนวณค่า BRI รอบแกน X กันนะครับ
BRI รอบแกน X = (Ix-x)/(I) x 100 = 2.40/3.25 x 100 = 73
ต่อมาเราจะมาคำนวณค่า BRI รอบแกน Y กันต่อครับ
BRI รอบแกน Y = (Iy-y)/(I) x 100 = 1.62/3.25 x 100 = 49
จาก ตย ข้อนี้เพื่อนๆ สังเกตอะไรหรือไม่ครับ ?
ขอเฉลยนะครับ จาก ตย ข้อนี้แสดงให้เห็นว่าค่า BRI รอบแกนแต่ละแกนอาจมีค่าไม่เท่ากันได้ โดยที่แกนที่มีค่า BRI มากกว่าก็คือด้านที่มีกำลังต้านทานการดัดที่สูงกว่าอีกแกนด้วย โดยหากแกนใดแกนหนึ่งมีค่าๆ นี้แตกต่างกันมากๆ จึงเป็นที่มาของคำว่าแกนหลักและแกนรองของโครงสร้างอาคารของเรานั่นเองครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากพี่แขก และ เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อยนะครับ จนกว่าจะพบกันใหม่
ADMIN JAMES DEAN