สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
กลับมาพบกันในทุกๆ วันเสาร์แบบนี้อีกครั้งหนึ่งซึ่งผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะพูดคุยกันถึงหัวข้อ “ถาม-ตอบชวนสนุก” กันนะครับ
โดยที่ในวันนี้ผมได้ทำการหยิบยกเอาคำถามที่มีความเกี่ยวข้องกันกับเรื่อง ความรู้ดีๆ เพื่อคุณผู้หญิง เอามาเป็นคำถามประจำสัปดาห์และเหมือนเช่นเคยผมคงจะต้องออกตัวอีกครั้งหนึ่งว่า คำถามประจำสัปดาห์นี้สุดแสนจะง่ายมากๆๆๆๆๆๆๆๆๆ โดยที่โจทย์ในวันนี้ก็คือ
หากผมมีคานรับแรงดัดที่จะต้องรับน้ำหนักบรรทุกดังที่ได้แสดงอยู่ในรูป โดยคานจะต้องรับน้ำหนักบรรทุกแบบกระทำโดยแผ่กระจายตัวสม่ำเสมอหรือ UNIFORMLY DISTRIBUTED LOAD มีค่าเท่ากับ 1,000 กิโลกรัมต่อเมตร และ จะต้องรับน้ำหนักบรรทุกแบบกระทำเพียงจุดเดียวหรือ CONCENTRATED LOAD มีค่าเท่ากับ 2,000 กิโลกรัม ทั้งนี้คานรับแรงดัดของเรานั้นจะมีความยาวช่วงเท่ากับ 6.00 เมตร และทำจากเหล็กรูปพรรณที่มีค่าโมดูลัสยืดหยุ่นเท่ากับ 2×10^(6) กิโลกรัมต่อตารางเซนติเมตร และ มีค่าโมดูลัสความเฉื่อยของหน้าตัดเท่ากับ 10,000 ซม^(4)
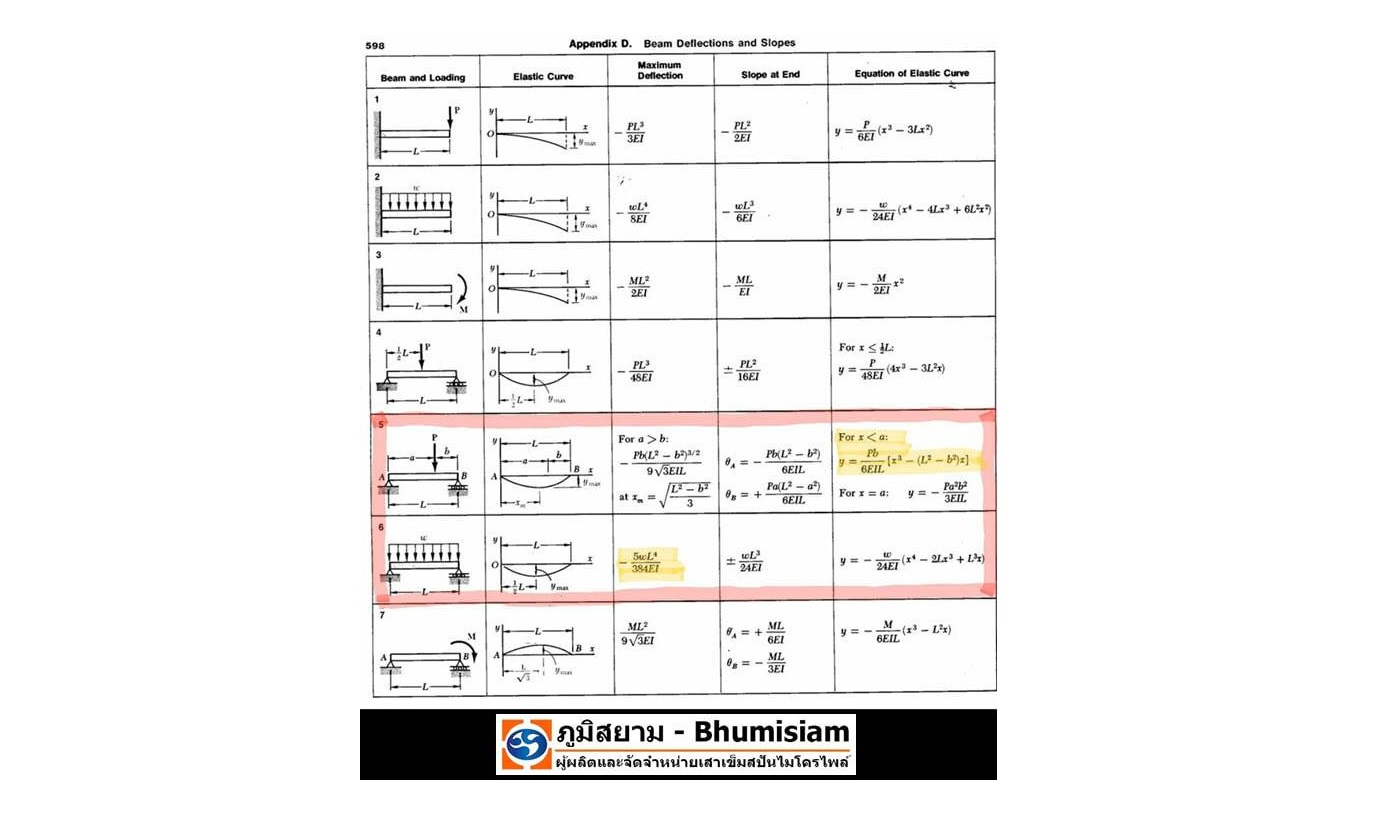
หากผมจะให้เพื่อนๆ นั้นอาศัยรูปแบบของตารางที่ผมได้ให้เอาไว้เมื่อวันอังคารที่ผ่านมา จงทำการคำนวณดูซิว่า คานรับแรงดัดของเรานั้นจะมีค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานเท่ากับเท่าใดครับ ?
ปล ผมขออนุญาตใบ้ให้เพื่อนๆ ไว้นิดหนึ่งนะครับว่า เพื่อนสามารถที่จะใช้หลักการของการ SUPERPOSITION ในการแก้ปัญหาข้อนี้ได้นะครับ
ยังไงเพื่อนๆ อย่าลืมนะครับ กติกาของการร่วมสนุกในเกมๆ นี้คือก่อนที่จะตอบ เพื่อนๆ จะต้องแจ้งอีเมลล์ของเพื่อนๆ ก่อนเสมอนะครับ มิเช่นนั้นผมจะถือว่าผิดกติกานะครับ ทั้งนี้เพื่อนๆ ยังสามารถที่จะให้เหตุผลต่างๆ หรือ อาจจะทำการสเก็ตช์ภาพประกอบคำตอบเพื่อใช้อธิบายเพิ่มเติมได้ แล้วยังไงวันพรุ่งนี้ผมจะขออนุญาตมาทำการเฉลยคำถามข้อนี้ให้แก่เพื่อนๆ ทุกคนได้รับทราบพร้อมๆ กันนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำถามในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันเสาร์
#ถามตอบชวนสนุก
#ปัญหาเรื่องการคำนวณหาค่าการโก่งตัวของคานรับแรงดัด
#การคำนวณค่าการโก่งตัวที่ตำแหน่งกึ่งกลางของช่วงความยาวของคาน
เฉลย
ซึ่งตามที่ผมได้บอกใบ้ให้กับเพื่อนๆ ไว้ในตอนท้ายด้วยว่า เพื่อนๆ สามารถที่จะใช้หลักการของการ SUPERPOSITION ในการแก้ปัญหาข้อนี้ได้ ซึ่งผมก็หมายความเช่นนั้นจริงๆ ยังไงเรามาติดตามดูเฉลยไปพร้อมๆ กันนะครับ
ก่อนอื่นเลยเราจะต้องมาดูก่อนว่าจากตารางที่ผมได้ให้ไว้ รูปใดที่จะตรงกับกรณีของการรับน้ำหนักของเราบ้าง ซึ่งคำตอบก็คือ กรณีในรูปย่อยที่ 5 และ 6 ซึ่งการที่ผมได้บอกใบ้ให้กับเพื่อนๆ ไว้ในตอนท้ายด้วยว่า เพื่อนๆ สามารถที่จะใช้หลักการของการ SUPERPOSITION ในการแก้ปัญหาข้อนี้ได้ก็เป็นเพราะว่า เราสามารถที่จะทำการรวมหรือ COMBINED รูปทั้ง 2 ให้เป็นดังกรณีรูปในปัญหาของเราได้เลยนั่นเอง ดังนั้นปัญหาข้อนี้ก็พอที่จะทำการสรุปได้ง่ายๆ ว่า ค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานนั้นจะมีค่าเท่ากับ Δ(c) ซึ่งก็จะมีค่าเท่ากับค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานในรูปย่อยที่ 5 หรือว่า Δ(c case 5) รวมกันกับค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานในรูปย่อยที่ 6 หรือว่า Δ(c case 6) หรือเขียนให้อยู่ในรูปแบบของสมการหลักง่ายๆ ได้ว่า
Δ(c) = Δ(c case 5) + Δ(c case 6)
ดังนั้นเราอาจจะเริ่มต้นทำการคำนวณแทนค่าเพื่อทำการหาค่าของ Δ(c case 5) และ Δ(c case 6) ตามลำดับ เพียงแต่ว่าสำหรับรูปย่อยที่ 5 นั้น เราจะต้องใช้สมการในรูปขวามือสุด โดยการแทนระยะของ X ด้วยระยะ L/2 เพราะหากใช้สมการในช่องของหลักที่ 3 ค่าที่ได้นั้นจะไม่ได้เป็นค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานเนื่องจากกรณีของน้ำหนักกระทำแบบจุดแต่จะได้เป็นค่าการโก่งตัวที่ “มากที่สุด” ของคานเนื่องจากกรณีของน้ำหนักกระทำแบบจุดแทนนะครับ
ต่อมาค่าต่างๆ ที่จะต้องถูกนำไปแทนค่าลงในสมการนั้นก็จะต้องถูกทำการแปลงให้อยู่ในหน่วยที่ตรงกันเสียก่อน ซึ่งในปัญหาข้อนี้ผมก็จะเลือกทำการแปลงให้หน่วยของแรงให้อยู่ในหน่วย กิโลกรัม (แรง) และหน่วยของความยาวให้อยู่ในหน่วย เซนติเมตร ดังนั้น
ค่าน้ำหนักบรรทุกแบบกระทำเพียงจุดเดียวหรือค่า P นั้นก็จะมีค่าเท่ากับ
P = 2,000 กิโลกรัม
ค่าน้ำหนักบรรทุกแบบกระทำโดยแผ่กระจายตัวสม่ำเสมอหรือค่า W นั้นก็จะมีค่าเท่ากับ
W = 1,000 กิโลกรัมต่อเมตร
W = 10 กิโลกรัมต่อเซนติเมตร
ค่าความยาวช่วงของคานหรือค่า L นั้นก็จะมีค่าเท่ากับ
L = 6.00 เมตร
L = 600 เซนติเมตร
ค่าความยาวช่วงที่ปลายด้านขวามือหรือค่า b นั้นก็จะมีค่าเท่ากับ
L = 2.00 เมตร
L = 200 เซนติเมตร
ค่าโมดูลัสยืดหยุ่นของเหล็กรูปพรรณหรือค่า E นั้นก็จะมีค่าเท่ากับ
E = 2 x 10^(6) กิโลกรัมต่อตารางเซนติเมตร
ค่าโมดูลัสความเฉื่อยของหน้าตัดหรือค่า I นั้นก็จะมีค่าเท่ากับ
I = 10,000 เซนติเมตร^(4)
ขั้นตอนสุดท้ายก็เหลือเพียงแต่การแทนค่าลงไปในสมการทั้งสอง ซึ่งสมการแรกก็จะออกมาเป็นค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานเนื่องจากกรณีของน้ำหนักกระทำแบบจุดออกมามีค่าเท่ากับ
Δ(c case 5) = P x b / (6 x E x I x L) { (L/2)^(3) – [L^(2) – b^(2)] x (L/2) }
Δ(c case 5) = 2,000 x 200 / (6 x 2 x 10^(6) x 10,000 x 600) { 300^(3) – [600^(2) – 200^(2)] x 300 }
Δ(c case 5) = – 0.383 เซนติเมตร
ส่วนสมการที่สองก็จะได้ออกมาเป็นค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานเนื่องจากกรณีของน้ำหนักกระทำแบบแผ่ออกมามีค่าเท่ากับ
Δ(c case 6) = – 5 x W x L^(4) /(384 x E x I)
Δ(c case 6) = – 5 x 10 x 600^(4) /(384 x 2 x 10^(6) x 10,000)
Δ(c case 6) = – 0.844 เซนติเมตร
ซึ่งสุดท้ายก็เพียงแค่ทำการแทนค่าลงไปในสมการหลักซึ่งก็คือ ค่าการโก่งตัวที่ “จุดกึ่งกลาง” ของคานเนื่องจากรูปแบบของน้ำหนักบรรทุกทั้งสองรูปแบบออกมา ซึ่งก็จะมีค่าเท่ากับ
Δ(c) = Δ(c case 5) + Δ(c case 6)
Δ(c) = (- 0.383) + (- 0.844)
Δ(c) = – 1.227 เซนติเมตร
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำตอบในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันอาทิตย์
#ถามตอบชวนสนุก
#ตอบปัญหาเรื่องการคำนวณหาค่าการโก่งตัวของคานรับแรงดัด
#เฉลยปัญหาการคำนวณค่าการโก่งตัวที่ตำแหน่งกึ่งกลางของช่วงความยาวของคาน
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com